
使用NestJS和Prisma構建REST API:身份驗證
模型解釋作為一個概念仍然主要是理論和主觀的。任何機器學習模型的核心都有一個響應函數,它試圖映射和解釋獨立 ( 輸入 ) 自變量和 ( 目標或響應 ) 因變量之間的關系和模式。當模型預測或尋找見解時,需要做出某些決定和選擇。模型解釋試圖理解和解釋響應函數所做出的這些決定,即 what,why 以及 how。模型解釋的關鍵是透明度,質疑能力以及人類理解模型決策的難易程度。模型解釋的三個最重要的方面解釋如下:
??是什么驅動了模型的預測?我們應該能夠查詢我們的模型并找出潛在的特征交互,以了解哪些特征在模型的決策策略中可能是重要的。這確保了模型的公平性。
??為什么模型會做出某個決定?我們還應該能夠驗證并證明為什么某些關鍵特征在預測期間驅動模型所做出的某些決策時負有責任。這確保了模型的可靠性。
??我們如何信任模型預測?我們應該能夠評估和驗證任何數據點以及模型如何對其進行決策。對于模型按預期工作的關鍵利益相關者而言,這應該是可證明且易于理解的。這確保了模型的透明度。
在比較模型時,除了模型性能之外,如果模型的決策比其他模型的決策更容易理解,那么模型被認為比其他模型具有更好的可解釋性。
在解決機器學習問題時,數據科學家往往傾向于關注模型性能指標,如準確性,精確度和召回等等 ( 毫無疑問,這很重要 ! )。這在大多數圍繞數據科學和機器學習的在線競賽中也很普遍。但是,指標只能說明模型預測決策的部分故事。隨著時間的推移,由于環境中的各種因素導致的模型概念漂移,性能可能會發生變化。因此,了解推動模型采取某些決策的因素至關重要。
如果一個模型工作得很好,為什么還要深入挖掘呢?在解決現實世界中的數據科學問題時,為了讓企業信任您的模型預測和決策,他們會不斷提出 “我為什么要相信您的模型?” 這一問題,這一點非常有意義。如果一個人患有癌癥或糖尿病,一個人可能對社會構成風險,或者即使客戶會流失,您是否會對預測和做出決策 ( 如果有的話 ) 感到滿意?也許不是,如果我們能夠更多地了解模型的決策過程 ( 原因和方式 ),我們可能會更喜歡它。這使我們更加透明地了解模型為何做出某些決策,在某些情況下可能出現的問題,并且隨著時間的推移它有助于我們在這些機器學習模型上建立一定程度的信任。
? 了解預測背后的原因在評估信任方面非常重要,如果計劃基于預測采取行動,或者選擇是否部署新模型,那么這是至關重要的。
? 無論人類是直接使用機器學習分類器作為工具,還是在其他產品中部署模型,仍然存在一個至關重要的問題:如果用戶不信任模型或預測,他們就不會使用它。
這是我們在本文中多次討論的內容,也是決定數據科學項目在行業中取得成功的關鍵區別之一。這推動了模型解釋的必要性和重要性的緊迫性。
有一些特定的標準可用于分類模型解釋方法。Christoph Molnar,2018年 “可解釋的機器學習,制作黑箱模型可解釋指南” 中提到了一個很好的指南。
??內在還是事后?內在可解釋性就是利用機器學習模型,該模型本質上是可解釋的 ( 如線性模型,參數模型或基于樹的模型 )。事后可解釋性意味著選擇和訓練黑匣子模型 ( 集合方法或神經網絡 ) 并在訓練后應用可解釋性方法 ( 特征重要性,部分依賴性圖 )。我們將更多地關注我們系列文章中的事后模型可解釋方法。
??模型特定或模型不可知?特定于模型的解釋工具非常特定于內在模型解釋方法,這些方法完全依賴于每個模型的功能和特征。這可以是系數,p 值,與回歸模型有關的 AIC 分數,來自決策樹的規則等等。與模型無關的工具與事后方法更相關,可用于任何機器學習模型。這些不可知方法通常通過分析 ( 和輸入的擾動 ) 特征輸入和輸出對來操作。根據定義,這些方法無法訪問任何模型內部,如權重,約束或假設。
??本地還是全局?這種解釋分類討論了解釋方法是解釋單個預測還是整個模型行為?或者如果范圍介于兩者之間?我們將很快談論全球和地方的解釋。
如何定義可解釋性的范圍和界限?一些有用的方面可以是模型的透明度,公平性和責任性。全局和局部模型解釋是定義模型解釋范圍的明確方法。
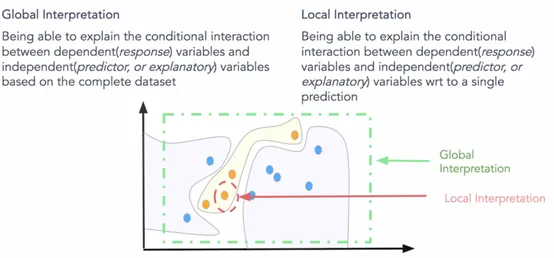
? 全局可解釋:就是試圖理解 “模型如何進行預測?” 和 “模型的子集如何影響模型決策?”。要立即理解和解釋整個模型,我們需要全局可解釋性。全局可解釋性是指能夠基于完整數據集上的依賴 ( 響應 ) 變量和獨立 ( 預測變量 ) 特征之間的條件交互來解釋和理解模型決策。嘗試理解特征交互和重要性始終是理解全球解釋的一個很好的一步。當然,在嘗試分析交互時,在超過兩維或三維之后可視化特征變得非常困難。因此,經常查看可能影響全局知識模型預測的模塊化部分和特征子集會有所幫助。全局解釋需要完整的模型結構,假設和約束知識。
? 局部解釋:試圖理解 “為什么模型為單個實例做出具體決策?” 和 “為什么模型為一組實例做出具體決策?”。對于本地可解釋性,我們不關心模型的固有結構或假設,我們將其視為黑盒子。為了理解單個數據點的預測決策,我們專注于該數據點并查看該點周圍的特征空間中的局部子區域,并嘗試基于該局部區域理解該點的模型決策。本地數據分布和特征空間可能表現完全不同,并提供更準確的解釋而不是全局解釋。局部可解釋模型 – 不可知解釋 ( LIME ) 框架是一種很好的方法,可用于模型不可知的局部解釋。我們可以結合使用全局和局部解釋來解釋一組實例的模型決策。
? 模型透明度:為試圖理解 “如何根據算法和特征創建模型?”。我們知道,通常機器學習模型都是在數據特征之上利用算法來構建將輸入映射到潛在輸出 ( 響應 ) 的表示。模型的透明度可能試圖了解模型的構建方式以及可能影響其決策的更多技術細節。這可以是神經網絡的權重,CNN 濾波器的權重,線性模型系數,決策樹的節點和分裂。但是,由于業務可能不太精通這些技術細節,因此嘗試使用不可知的局部和全局解釋方法來解釋模型決策有助于展示模型透明度。
對于想要了解模型如何工作的數據科學家來說,評估模型的準確性通常是不夠的。數據科學家通常想知道模型輸入變量如何工作以及模型的預測如何根據輸入變量的值而變化。
機器學習算法和模型的工程應用中用到最多的主要是樹類模型 (lgb, xgb) 和神經網絡 (cnn, rnn),使用者往往習慣于很少去思考其中的含義和解釋性。需要思考一個模型的哪些東西是可解釋的?所以有幾個問題值得討論:
??哪些特征在模型看到是最重要的?
??關于某一條記錄的預測,每一個特征是如何影響到最終的預測結果的?
??從大量的記錄整體來考慮,每一個特征如何影響模型的預測的?
為什么這些解釋信息是有價值的呢?
? 調試模型用。一般的真實業務場景會有很多不可信賴的,沒有組織好的臟數據。你在預處理數據時就有可能加進來了潛在的錯誤,或者不小心泄露了預測目標的信息等,考慮各種潛在的災難性后果,debug 的思路就尤其重要了。當你遇到了用現有業務知識無法解釋的數據的時候,了解模型預測的模式,可以幫助你快速定位問題。
? 指導工程師做特征工程。特征工程通常是提升模型準確率最有效的方法。特征工程通常涉及到到反復的操作原始數據 ( 或者之前的簡單特征 ),用不同的方法來得到新的特征。有時候你完成FE的過程只用到了自己的直覺。這其實還不夠,當你有上百個原始特征的時候,或者當你缺乏業務背景知識的時候,你將會需要更多的指導方向。如何創造出這樣優秀的特征呢?如何找到最重要的特征的方法,并且可以發現兩個特別相關的特征,當面對越來越多的特征的時候,這些方法就會很重要啦。
? 指導數據采集的方向。對于網上下載的數據集你完全控制不了。不過很多公司和機構用數據科學來指導他們從更多方面收集數據。一般來說,收集新數據很可能花費比較高或者不是很容易,所以大家很想要知道哪些數據是值得收集的。基于模型的洞察力分析可以教你很好的理解已有的特征,這將會幫助你推斷什么樣子的新特征是有用的。
? 指導人們做決策。一些決策是模型自動做出來的,雖然亞馬遜不會用人工來決定展示給你網頁上的商品,但是很多重要的決策是由人來做出的,而對于這些決定,模型的洞察力會比模型的預測結果更有價值。
? 建立模型和人之間的信任。很多人在做重要決策的時候不會輕易的相信模型,除非他們驗證過模型的一些基本特性,這當然是合理的。實際上,把模型的可解釋性展示出來,如果可以匹配上人們對問題的理解,那么這將會建立起大家對模型的信任,即使是在那些沒有數據科學知識的人群中。
? Confusion Matrix
一個完美的分類模型就是,如果一個客戶實際上屬于類別 good,也預測成 good,處于類別 bad,也就預測成 bad。實際上一些是 good 的客戶,根據我們的模型,卻預測他為 bad,對一些原本是 bad 的客戶,卻預測他為 good。我們需要知道,這個模型到底預測對了多少,預測錯了多少,混淆矩陣就把所有這些信息,都歸到一個表里:
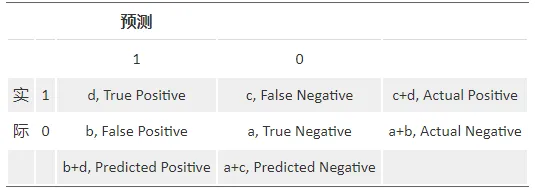
Sensitivity (覆蓋率,True Positive Rate) = 正確預測到的正例數 / 實際正例總數;Recall (True Positive Rate, or Sensitivity) = true positive/total actual positive = d/c+d;
PV+ (命中率,Precision, Positive Predicted Value) = 正確預測到的正例數 / 預測正例總數;Precision (Positive Predicted Value, PV+) = true positive/ total predicted positive = d/b+d;
Specificity (負例的覆蓋率,True Negative Rate) = 正確預測到的負例個數 / 實際負例總數;Specificity (True Negative Rate) = true negative/total actual negative = a/a+b;
圖中關于混淆矩陣結果理解:recall:0.54;precision:0.915;specificity:0.95。
? Lift
它衡量的是,與不利用模型相比,模型的預測能力 “變好” 了多少。實質上它強調的是投入與產出比。不利用模型,我們只能利用 “正例的比例是 c+d/a+b+c+d” 這個樣本信息來估計正例的比例 ( baseline model ),而利用模型之后,我們不需要從整個樣本中來挑選正例,只需要從我們預測為正例的那個樣本的子集 ( b+d ) 中挑選正例,這時預測的準確率為 d/b+d。
顯然,lift ( 提升指數 ) 越大,模型的運行效果越好。如果這個模型的預測能力跟 baseline model 一樣,那么 d/b+d 就等于 c+d/a+b+c+d ( lift 等于 1 ),這個模型就沒有任何 “提升” 了 ( 套一句金融市場的話,它的業績沒有跑過市場 )。
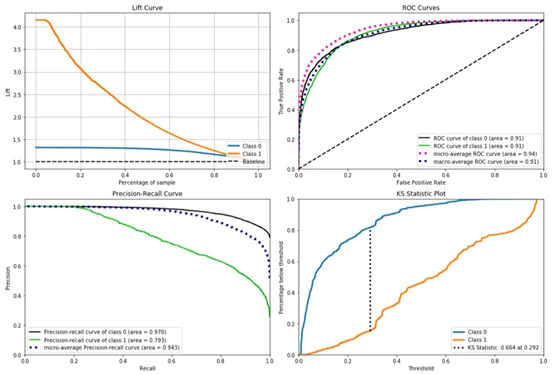
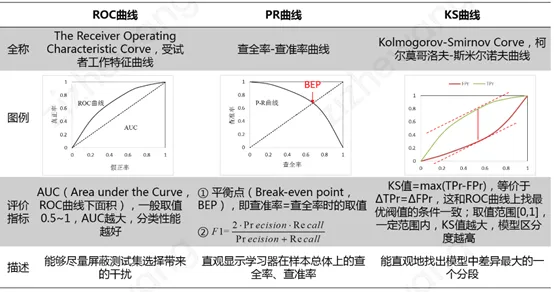
? ROC 曲線 & PR 曲線 & KS 曲線
實際應用中,通常是先基于訓練好的分類器得出測試樣本的預測概率,然后將該測試樣本的預測概率與給定的閾值進行比較,若該預測概率大于給定閾值,則將該測試樣本劃分為正類,反之則將其劃分為反類。對于不同的分類任務,該分類閾值的取值也是不一樣的。
① ROC 曲線 ( The Receiver Operating Characteristic Curve ) 給出的是不同分類閾值情況下真正率 ( TPr ) 和假正率 ( FPr ) 的變化曲線。
② PR 曲線 ( Precision-Recall Curve ) 給出的是不同分類閾值情況下查準率 ( Precision ) 和查全率 ( Recall ) 的變化曲線。
有文獻指出,ROC 曲線相比 PR 曲線有一個非常好的特性:就是當正負樣本分布發生變化的時候,ROC 曲線的形狀能夠基本保持不變,而 PR 曲線的形狀會發生較劇烈的變化。為了使得 ROC 曲線之間能更好的進行比較,通常采用 AUC,即 ROC 曲線下的面積來衡量一個分類算法的性能。其中,AUC 的值越大,表明分類性能越好。
③ KS ( Kolmogorov-Smirnov Curve ) 曲線橫軸為不同的分類閾值,縱軸為真正率 ( TPr ) 和假正率 ( FPr ) 的變化曲線。KS 值 = max|TPr-FPr|,等價于 ΔTPr=ΔFPr,這和 ROC 曲線上找最優閾值的條件一致。KS 值常在征信評分模型中用于衡量區分預測正負樣本的分隔程度。一般來說,KS 值越大,表明正負樣本區分的程度越好,說明模型區分度越高。但并非所有的情況 KS 值都是越高越好的,尤其在征信模型中,如正負樣本完全分錯的情況下,KS 值依舊可以很高。征信模型最期望得到的信用分數分布為正態分布,如果 KS 值過大,如0.9,就可以認為正負樣本分得過開了,不太可能是正態分布,反而比較可能是極端化的分布狀態 ( 如 U 字型 ),這樣的分數就很不好,基本可以認為不可用。
? Cumulative gains chart
橫坐標表示:代表我們樣本的百分比,假設有10000個樣本,0.1代表1000個,1代表10000個樣本。
縱坐標表示:代表橫軸所代表的那么多樣本中,判斷正確的比率。
baseline 表示:如果我們不用模型,那我們對每一個人的打分都是一樣的,正率在所有樣本空間都是一樣的,連接起來就成為一條直線。
曲線含義:采用模型進行預測。y 值的分子代表模型預測且預測為正例的人數,分母是整個群體正例人數。
? Silhouette Analysis
Silhouette 指的是一種解釋和驗證數據集群內一致性的方法。該技術提供了每個對象分類的簡潔圖形表示。
輪廓值是對象與其自身群集 ( 內聚 ) 相比與其他群集 ( 分離 ) 相似程度的度量。輪廓范圍從-1到+1,其中高值表示對象與其自己的簇很好地匹配并且與相鄰簇很不匹配。如果大多數對象具有高值,則群集配置是合適的。如果許多點具有低值或負值,則群集配置可能具有太多或太少的群集。
圖中通過 Silhouette 方法大致對數據集樣本分類有了掌握,可以看到0/1類別大致比例。
? Learning Curve
概念:學習曲線就是通過畫出不同訓練集大小時訓練集和交叉驗證的準確率,可以看到模型在新數據上的表現,進而來判斷模型是否方差偏高或偏差過高,以及增大訓練集是否可以減小過擬合。
Bias 是用所有可能的訓練數據集訓練出的所有模型的輸出的平均值與真實模型的輸出值之間的差異。
Variance 是不同的訓練數據集訓練出的模型輸出值之間的差異。
解讀:當訓練集和測試集的誤差收斂但卻很高時,為高偏差。左上角的偏差很高,訓練集和驗證集的準確率都很低,很可能是欠擬合。我們可以增加模型參數,比如,構建更多的特征,減小正則項。此時通過增加數據量是不起作用的。當訓練集和測試集的誤差之間有大的差距時,為高方差。當訓練集的準確率比其他獨立數據集上的測試結果的準確率要高時,一般都是過擬合。右上角方差很高,訓練集和驗證集的準確率相差太多,應該是過擬合。我們可以增大訓練集,降低模型復雜度,增大正則項,或者通過特征選擇減少特征數。理想情況是是找到偏差和方差都很小的情況,即收斂且誤差較小。擴展閱讀:一文深度解讀模型評估方法
一個最基本的問題大概會是什么特征對我模型預測的影響最大呢?這個東西就叫做 “feature importance” 即特征重要性。Anyway,字面意思看著就很重要啦。我們有很多方法來衡量特征的重要性,這里呢,將會介紹一種方法:排列重要性。這種方法和其他方法比起來,優勢有:? 計算速度快? 廣泛使用和理解? 我們希望特征重要性與屬性具有一致性
工作原理:排列重要性,一定是在 model 訓練完成后,才可以計算的。簡單來說,就是改變數據表格中某一列的數據的排列,保持其余特征不動,看其對預測精度的影響有多大。大概三個步驟:
? 訓練好模型
? 拿某一個 feature column,然后隨機打亂順序。然后用模型來重新預測一遍,看看自己的 metric 或者 loss 。Function 變化了多少。
? 把上一個步驟中打亂的 column 復原,換下一個 column 重復上一個步驟,直到所有 column 都算一遍。
代碼示例:
from xgboost import XGBClassifier
from sklearn.model_selection import train_test_split
import eli5 # python計算permutation importance工具包
from eli5.sklearn import PermutationImportance
path = './census_income_dataset.csv'
data = pd.read_csv(path)
#...省略數據預處理過程
X_train, X_test, y_train, y_test = train_test_split(df, y, test_size=0.2, random_state = 400)
# 訓練XGBoost模型
model = xgb.XGBClassifier(
learning_rate =0.05,
n_estimators=100,
max_depth=3,
min_child_weight=1,
gamma=0.3,
subsample=0.8,
colsample_bytree=0.8,
objective= 'multi:softprob',
nthread=4,
scale_pos_weight=1,
num_class=2,
seed=27
).fit(X_train, y_train)
perm = PermutationImportance(model, random_state = 1).fit(X_test, y_test) # 實例化
eli5.show_weights(perm, feature_names = X_test.columns.tolist())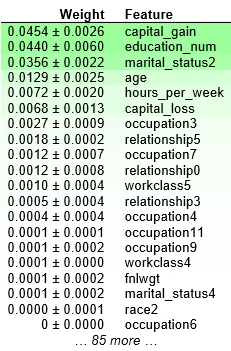
結果分析:
? 靠近上方的綠色特征,表示對模型預測較為重要的特征;
? 為了排除隨機性,每一次 shuffle 都會進行多次,然后取結果的均值和標準差;
? 部分特征出現負值,表示其 shuffle 之后,對精度反而有所提升。這通常出現在特征不那么重要的時候。當數據集較小的時候,這種情況更為常見;
? “+ -” 之后的數字衡量的是一次重新洗牌后的表現如何變化。
這個數據集是收入水平數據集,這個例子里,最重要的特征是 “capital_gain”,這看起來是合理的。
部分依賴圖 ( PDP 或 PD 圖 ) 顯示特征對機器學習模型的預測結果的邊際效應,可以展示一個特征是如何影響預測的。部分依賴圖可以顯示目標與特征之間的關系是線性的,單調的還是更復雜的。例如,當應用于線性回歸模型時,部分依賴圖總是顯示線性關系。回歸的部分依賴函數定義為:
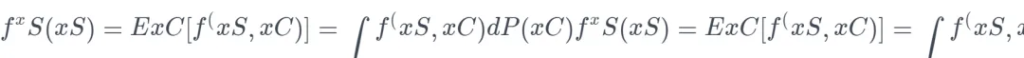
? xSxS 是部分依賴圖要畫的特征集合
? xCxC 是其他特征
通常,集合 SS 中有一到兩個特征,這個集合中的特征我們想知道他們對預測的影響。在集合 SS 和集合 CC 中的特征并集組成了全部特征空間 x。邊際化機器學習模型輸出在集合 C 的特征分布上。PDP 的一個假設是,C 中的特征與 s 中的特征不相關。如果違反這個假設,部分依賴圖的平均值將包括非常不可能甚至不可能的數據點。
邊緣化概念
邊緣化是一種通過累加一個變量的可能值以判定另一個變量的邊緣分布的方法。這聽起來有點抽象,讓我們看一個例子:
假設我們想知道天氣是如何影響英國人的幸福感的,也就是 P ( 幸福感|天氣 )。假定我們具有衡量某人的幸福感所需的定義和設備,同時記錄了某個英格蘭人和某個蘇格蘭人所處位置的天氣。可能蘇格蘭人通常而言要比英格蘭人幸福。所以我們其實在衡量的是 P ( 幸福感, 國|天氣 ),即,我們同時考察幸福感和國。
邊緣化告訴我們,我們可以通過累加國家的所有可能值 ( 英國由3國組成:英格蘭、蘇格蘭、威爾士 ),得到想要計算的數字,即 P ( 幸福感|天氣 ) = P ( 幸福感, 國=英格蘭|天氣 ) + P ( 幸福感, 國=蘇格蘭|天氣 ) + P ( 幸福感, 國=威爾士|天氣 )。部分函數 f^xSf^xS 通過計算在訓練數據的平均值,即 Monte Carlo 方法:
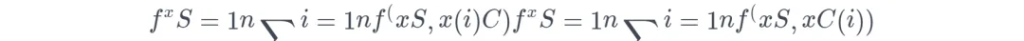
x(i)CxC(i) 是數據集中的真實特征值,這些特征是不關注的特征。
特征重要性可以告訴你哪些特征是最重要的或者是不重要的。
partial dependence 圖可以告訴你一個特征是如何影響預測的。
PDP 分析步驟如下:
? 訓練一個 Xgboost 模型 ( 假設 F1 … F4 是我們的特征,Y 是目標變量,假設 F1 是最重要的特征 )。
? 我們有興趣探索 Y 和 F1 的直接關系。
? 用 F1 ( A ) 代替 F1 列,并為所有的觀察找到新的預測值。采取預測的平均值 ( 稱之為基準值 )。
? 對 F1 ( B ) … F1 ( E ) 重復步驟3,即針對特征 F1 的所有不同值。
? PDP 的 X 軸具有不同的 F1 值,而 Y 軸是雖該基準值 F1 值的平均預測而變化。
PDP 特別適合用來回答類似這樣的問題:
? 在所有的收入水平的特征中,年齡和學歷是如何影響收入的?或者說,在不同的國家相同年齡的人群收入水平有多少相似呢?
? 預測推薦基金時,投資偏好的不同會帶來多大的影響?還是有其他更重要的影響因素?
如果你對線性回歸或者邏輯回歸比較熟悉,那么 partial dependence 可以被類比為這兩類模型中的 “系數”。并且 partial dependence 在復雜模型中的作用比在簡單模型中更大,抓出更復雜的特性。
同樣還是用 census_income 的數據集,不同的個體在各個方面都是不一樣的。比如種族,年齡,受教育程度等等。一眼看過去,很難區分這些特征對結果的影響有多大。為了清晰的分析,我們還是先只拿出某一行數據,比如說這一行數據里,有種族 White,45歲,Bachelors。我們將會用已有模型來預測結果,將這一行的某一個變量,反復的進行修改和重新預測,比如將年齡修改從45修改為60,等等。持續觀察預測結果,在不同的年齡時有什么樣的變化。
這里的例子,只用到了一行數據。特征之間的相互作用關系通過這一行來觀察可能不太妥當,那么考慮用多行數據來進行試驗,然后根據平均值畫出圖像來。
from pdpbox import pdp
feature = 'age'
# 創建好畫圖所需的數據
pdp_goals = pdp.pdp_isolate(model, X_train, df.columns, feature)
# 畫出“age”這一特征的partial dependence plot
pdp.pdp_plot(pdp_goals, feature)
plt.show()
??y 軸是預測結果的變化量。??藍色陰影區域代表了置信的大小。
從這幅圖可以看出,age 的增加肯定可以增加高收入概率,但是增加到一定的時候,對這個概率影響不大了。
置信區間概念
給定置信水平,根據估計值確定真實值可能出現的區間范圍,該區間通常以估計值為中心,該區間則為置信區間。
feature = 'education_num'
pdp_goals = pdp.pdp_isolate(model, X_train, df.columns, feature)
pdp.pdp_plot(pdp_goals, feature)
plt.show()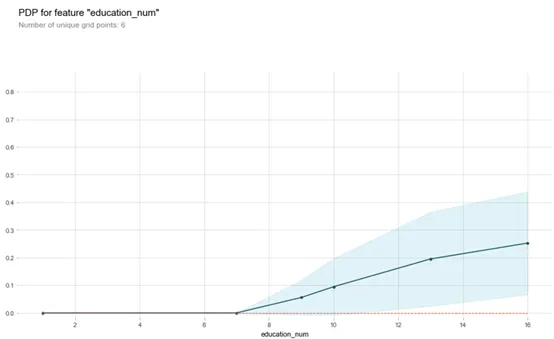
從這副圖可以看出,受教育程度對收入起積極作用,隨著受的教育越多,收入越高,也符合常人理解。
fig, axes, summary_df_1 = info_plots.target_plot_interact(
df=dataset, features=['age', 'education_num'], feature_names=['age', 'education_num'], target='income_level'
)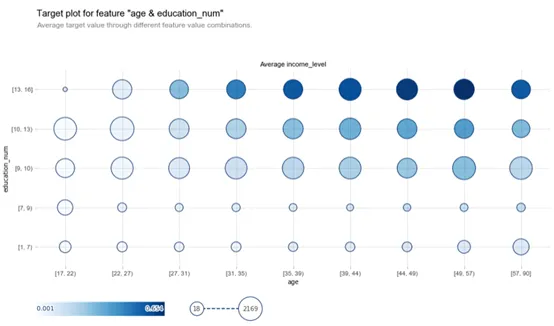
在此圖表中,氣泡大小不太重要,因為它與觀測數量 ( 事件發生的次數 ) 有關。最重要的見解來自氣泡的顏色,較暗的氣泡意味著更高的默認概率。這是一個強大的工具,因為它可以深入了解我們選擇的兩個變量對因變量的影響。
features_to_plot = ['age', 'education_num']
inter1 = pdp.pdp_interact(model, df, df.columns, features_to_plot)
pdp.pdp_interact_plot(inter1, features_to_plot, plot_type='grid', x_quantile=True, ncols = 2, plot_pdp=True)
plt.show()
上圖可以看出,受教育程度和年齡對收入水平有著正相關作用,且隨著受教育程度增加,年齡從35-90,高收入的概率越來越大。
fig, axes = pdp.pdp_interact_plot(
inter1, ['age', 'education_num'], plot_type='contour', x_quantile=True, ncols=2,
plot_pdp=True
)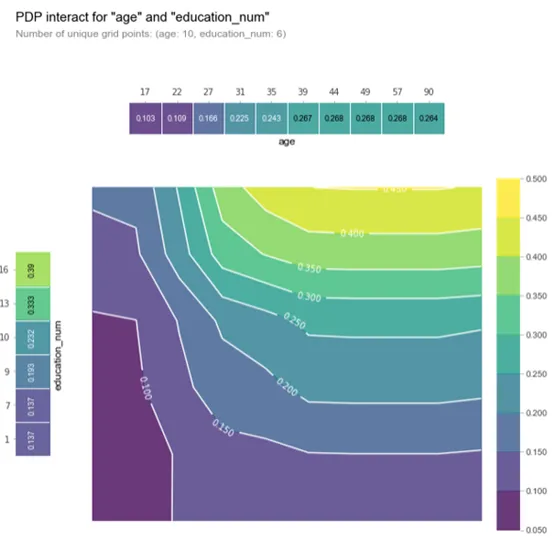
重要的是要記住,在該圖中,較暗的顏色并不一定意味著較高的默認概率。在這里,我們繪制了受教育等級和年齡與收入等級概率。我們可以推斷,在這兩個自變量中,education_num 起著更重要的作用,因為等高線圖主要是垂直的,遵循x軸刻度標記 ( 至少達到一個點 )。
部分依賴圖 ( PDP ) 和個體條件期望圖 ( ICE ) 說明了一個或多個輸入變量與黑盒模型的預測結果之間的關系。它們都基于可視化,模型不可知的技術。ICE 圖可以更深入地探索個體差異并識別模型輸入之間的子組和相互作用。
另一方面,ICE 圖使得可以深入到單個觀察的水平。它們可以幫助探索個體差異,并確定模型輸入之間的子組和交互。可以將每個 ICE 曲線視為一種模擬,顯示如果改變特定觀察的一個特征,模型預測會發生什么。為避免可視化過載,ICE 圖一次只顯示一個模型變量。
可以將每個 ICE 曲線視為一種模擬,顯示如果您改變特定觀察的一個特征,模型預測會發生什么。如圖9所示,通過在曲線變量的唯一值上復制個體觀察并對每個重復進行評分,獲得一個觀察的 ICE 曲線。
下圖中的 PD 圖結果基本上是平坦的,給人的印象是 X1 與模型的預測之間沒有關系。
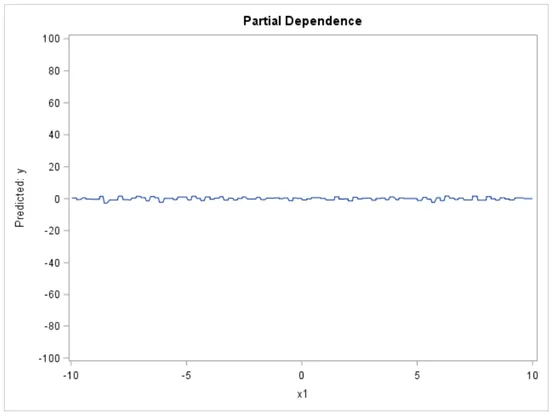
當我們觀察 ICE 圖時,它們呈現出一幅截然不同的圖:這種關系對于一次觀察非常正面,但對另一次觀察則非常負面。因此,與 PD 圖告訴我們的情況相反,ICE 圖顯示 X1 實際上與目標有關。基本上,ICE 圖分離 PD 功能 ( 畢竟是平均值 ) 以揭示相互作用和個體差異。
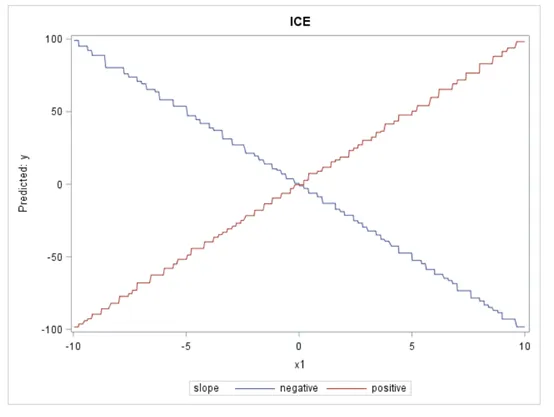
當對大數據集分析時,則可能需要進行一些調整。例如,可以對選定的變量進行分箱,也可以對數據集進行采樣或分組。這些技術可以更快地提供實際圖的合理近似值。
如果想進一步了解 PD 和 ICE 圖,Ray Wright 寫了一篇很好的論文,展示了 PD 和 ICE 圖如何用于比較和獲得機器學習模型的洞察力,特別是所謂的 “黑盒” 算法,如隨機森林,神經網絡和梯度增強。在他的論文中,他還討論了 PD 圖的局限性,并提供了有關如何為大數據生成可縮放圖的建議。
https://www.sas.com/content/dam/SAS/support/en/sas-global-forum-proceedings/2018/1950-2018.pdf
局部可解釋不可知模型 ( LIME ) 是一種算法,它提供了一種新穎的技術,以可解釋和可信任的方式解釋任何預測模型的結果。它的工作原理是圍繞想要解釋的預測在本地訓練可解釋的模型。這個工作發表于2016年 KDD 的論文。工具學習地址。
http://sameersingh.org/files/papers/lime-kdd16.pdf
https://lime-ml.readthedocs.io/en/latest/lime.html
流程:
? 訓練模型,模型 ( 記作 ff ) 可以是 LR、NN、Wide and deep、C4.5 Decision tree、Random forest、GBDT 等任意模型。
? 訓練結束后我們需要解析模型,先選擇一個待解析的樣本,樣本通過模型計算可以得到一個 prediction ( 包含預測的 label 以及預測為1的 probability ),這時我們在這個樣本的附近選擇新的樣本并用模型計算出多個 prediction,這樣樣本組合新的樣本集。
? 然后使用新的可解析的特征和 prediction 作為 label 來訓練新的簡單模型 ( 例如 LR ),然后使用簡單模型的權重作為這些特征的重要性作為輸出。
通俗來說:
就是選擇一個樣本以及樣本附近的點,然后訓練一個簡單模型來擬合,雖然簡單模型不能在完整數據集上有效,但至少在這個點附近都是有效的,這個簡單模型的特征是人類可解析的,而訓練出的權重也可以表示特征重要性。
論文中算法描述:

為了更好地理解 LIME 的工作原理,讓我們考慮兩種不同類型的可解釋性:
? 全局可解釋性:全局解釋有助于我們理解由訓練的響應函數建模的整個條件分布,但全局解釋可以是近似的或基于平均值。
? 局部可解釋性:局部解釋促進對單個數據點或分布的小范圍的理解,例如一組輸入記錄及其相應的預測。由于小范圍的條件分布很可能是線性的,因此局部解釋可能比全局解釋更準確。LIME 旨在提供局部可解釋性,因此對于特定決策或結果最為準確。
我們希望解釋器與模型無關,并且在局部可靠。局部可靠的解釋捕獲要解釋的實例鄰域中的分類器行為。為了學習局部解釋,LIME 使用可解釋的模型近似分類器圍繞特定實例的決策邊界。LIME 與模型無關,這意味著它將模型視為黑盒子,并且不對模型行為做出任何假設。這使得 LIME 適用于任何預測模型。
LIME 的核心在于三個方面:
? 這里不對模型整體提供解釋,而是局部對每一個樣本單獨進行解釋
??即使機器學習模型訓練過程會產生一些抽象的特征,但是解釋基于當前輸入數據的變量特征
? 通過局部建立簡單模型進行預測來對大多數重要特征進行解釋
LIME 作用在單個樣本上。
首先,我們取出一個樣本,并 ( permute ) 重復這個數據同時增加一些微小擾動,這樣就得到了一個新的數據集,數據集中包含相似的樣本,都基于取出來的那個樣本。對于這個新數據集中的每一個樣本,我們可以計算它跟取出的樣本之間的相似性,即在 permutation 中它被調整了多大,所有的統計距離、相似性矩陣都可以用在這里,比如用指定寬度的指數內核將歐式距離轉化為相似度。
下一步,使用最初訓練的復雜模型,在新數據上進行預測。正因為新數據樣本間的細微差別,我們可以跟蹤那些微小擾動對預測結果的影響。
最后,我們在新數據上訓練出一個簡單模型 ( 通常是線性模型 ),并使用最重要的特征進行預測。最重要的特征有不同的決定方法,在指定加入模型解釋中的特征數量 ( 通常在5到10附近 ) 的前提下,可以:
??選擇在使用復雜模型進行預測時回歸擬合上具有最高權重的特征
??運用正向選擇,選擇可以提高復雜模型的預測的回歸擬合的變量
??在復雜的機器學習模型預測的基礎上,選擇正則化的收縮率最小的 lasso 預測擬合的特征??使用不多于我們已經選擇了的特征的節點數量來構建決策樹
## 創建LIME解釋器
explainer = lime.lime_tabular.LimeTabularExplainer(X_train ,feature_names = features_name, class_names=['0','1'], categorical_features=data_cat_features,
categorical_names=cat_columns, kernel_width=3)
predict_fn_xgb = lambda x: xgb.predict_proba(x).astype(float)
exp = explainer.explain_instance(X_test[2], predict_fn_xgb, num_features=6)
exp.show_in_notebook(show_all=False)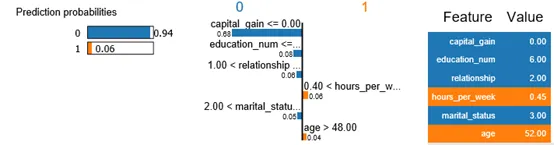
上圖給我們解釋了對于一個樣本的預測結果,是哪些特征決定樣本被分類到類別0,哪些特征決定樣本被分類到類別1,且具體列出樣本在這些特征的數值大小。很直觀和明確的解釋為什么模型做這個決定。
Shaply 值由美國洛杉磯加州大學教授羅伊德·夏普利 ( Lloyd Shapley ) 提出,用于解決合作博弈的貢獻和收益分配問題。N 人合作中,單個成員的貢獻不一樣,收益分配也應該不一樣。理想的分配方式是:貢獻=收益;
貢獻和收益分配是否有可以量化的方法呢?
Shapley 方法就是這樣一種方法:Shapley 值 ( 單個成員所得與自己的貢獻相等)。
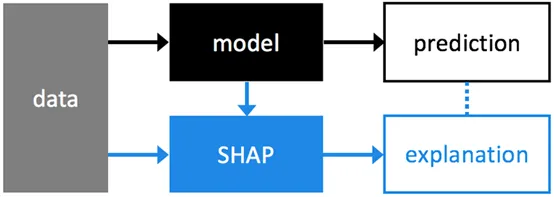
基于 Shap 值的模型解釋是一種和模型無關的方法。如上圖,模型預測和 Shap 值解釋是兩個并行流程,Shap 對模型預測的結果進行解釋。NIPS 論文地址:A Unified Approach to Interpreting Model Predictions,也可以參考這篇博客:One Feature Attribution Method to (Supposedly) Rule Them All: Shapley Values。
原理:一個特征的 shapley value 是該特征在所有的特征序列中的平均邊際貢獻。優點:
? 解決了多重共線性問題;
? 不僅考慮單個變量的影響,而且考慮變量組的影響,變量之間可能存在協同效應。
缺點:計算效率低。適用范圍:? 計算個體的特征 shapley value;? 所有個體的每個特征的 shapley value 的絕對值求和或求平均即為整體的特征重要性。
Shap 方法的兩大特性:
? 特征歸因 ( 收益 ) 一致性:
定義:模型改變 ( A->B ),特征 x 的貢獻不遞減 ( 增加或者保持現狀 ),則歸因 ( 收益 ) 也不遞減。
特點:特征作用越大 ( 小 ),重要度越高 ( 低 ),和模型變化無關。
全局特征一致性:① mean(|Tree SHAP|):Shap 值② Gain:特征用于劃分時所帶來的訓練損失減益的平均值③ Split Count:根據特征用于劃分的次數計算重要性④ Permutation:將特征的值隨機排列,用排列前后的模型誤差來計算重要性局部樣本 ( Fever=yes, cough=yes 的樣本 ) 一致性
① Saabas[5] : 樹創建完成后,根據樣本預測值,將父節點和子節點 value 的差異,作為父節點的特征重要性
② Tree SHAP : 基于 Shap 值矩陣 ( 樣本數*特征數 ),計算出 Fever 和 Cough 的重要性
? 特征歸因 ( 收益 ) 可加性:
解釋性方法如果具有特征歸因可加性,特征重要性和模型預測值可以通過特征貢獻的線性組合來表示。簡單模型最好的解釋是它本身;復雜模型,直接進行解釋并不容易,需要通過代理模型來解釋。接下來引入代理模型 ( 解釋模型 ) 來描述特征歸因可加性。
樹模型 Shap 值的解:
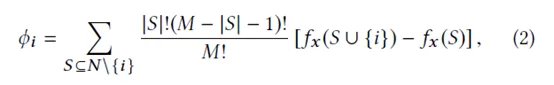
① N 為全體特征集合,S 為 N 的一個排列子集 ( 順序相關 )
② 求和第一項:排列數
③ 求和第二項:對于任意子集 S,特征i的貢獻
④ 特征 i 的 shap 值可以理解為i的貢獻歸因
詳細內容參考論文。
用 Shap 值識別特征交叉
Shap 方法計算兩兩特征交叉影響:
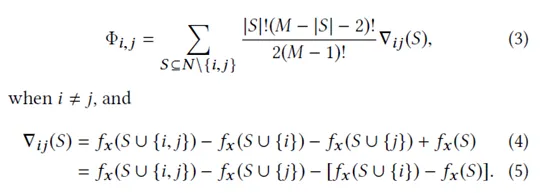
通俗理解:交叉影響=兩個人合作貢獻增益,減去各自單干的貢獻;
單個特征的貢獻
Shap 方法計算單個特征的貢獻 ( 剔除交叉影響 ):
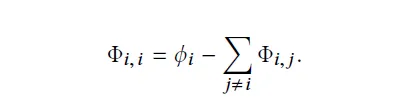
通俗理解:個人影響=個人合作貢獻,減去其它 N-1 個人的貢獻。下面還是以收入水平數據集進行案例分析:
row_to_show = 5
data_for_prediction = X_test.iloc[row_to_show] # use 5 row of data here. Could use multiple rows if desired
data_for_prediction_array = data_for_prediction.values.reshape(1, -1)
# 計算model的shap值
explainer = shap.TreeExplainer(model)
# 計算樣本數據的shap值
shap_values = explainer.shap_values(data_for_prediction)
shap.initjs()
shap.force_plot(explainer.expected_value[1], shap_values[1], data_for_prediction)
圖形解釋
① Base value:模型在數據集上的輸出均值:-0.1524
② Output value:模型在單個樣本的輸出值:0.68
③ 起正向作用的特征:marital_status2、occupation3
④ 起負向作用的特征:capital_gain、education_num
特征解釋
① 解釋 Output value ( 單個樣本 ) 和 Base value ( 全體樣本 Shap 平均值 ) 的差異,以及差異是由哪些特征造成的
② 紅色是起正向作用的特征,藍色是起負向作用的特征
shap_values_b = explainer.shap_values(X_test)
shap.force_plot(explainer.expected_value[0], shap_values_b[0], X_test, link="logit")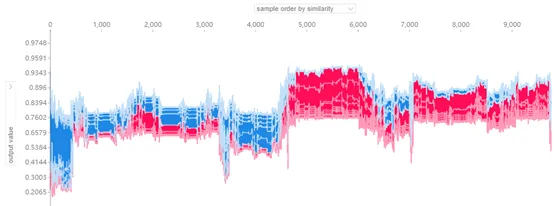
特征解釋
解釋 Output value 和 Base value 的差異,以及差異是由哪些特征造成的。
Summary Plots:
shap_values = explainer.shap_values(X_test)
shap.summary_plot(shap_values[1], X_test)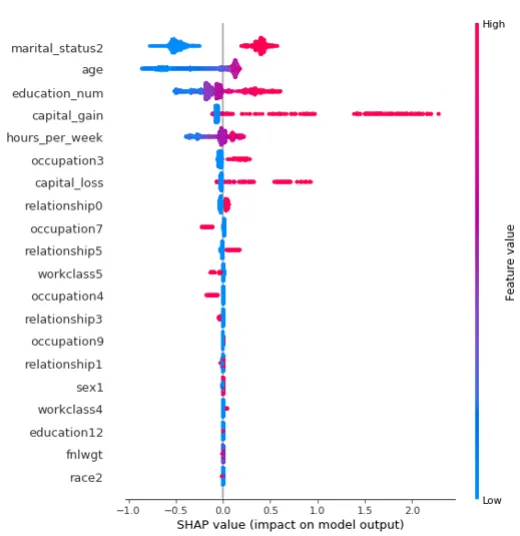
圖形解釋
① 每個點是一個樣本 ( 人 ),圖片中包含所有樣本
② X軸:樣本按 Shap 值排序-
③ Y軸:特征按 Shap 值排序
④ 顏色:特征的數值越大,越紅特征解釋:
martial_status2 這個特征最重要,且值越大,收入會相對更高,到達一定峰值,會明顯下降。
年齡也是影響結果的重要特征,年齡小收入普遍低,但年齡到達一定程度,并不會增加收入,存在年齡小,收入高的人群。
收入水平和 capital_gain 大致呈正相關。
shap.summary_plot(shap_values[1],X_test, plot_type="bar")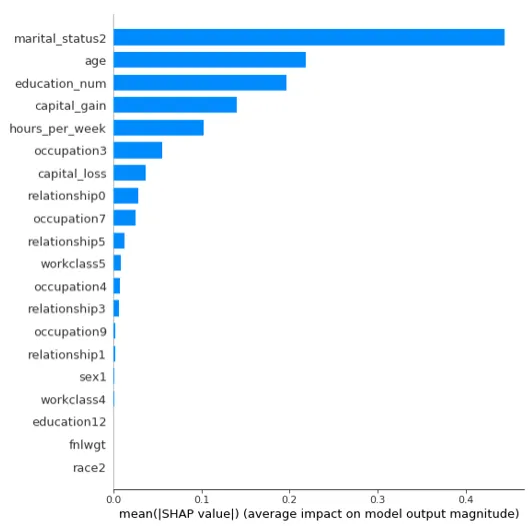
上圖是特征重要性圖譜,由上向下重要性依次減弱。
shap_values = explainer.shap_values(df)
shap.dependence_plot('age', shap_values[1], df, interaction_index="capital_gain")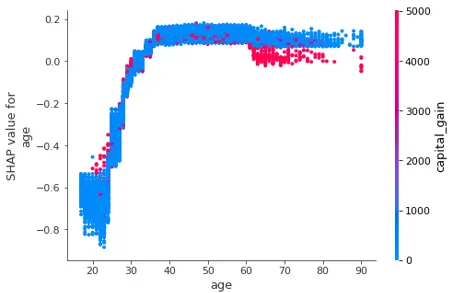
圖形解釋:
① X軸:age
② Y軸(左):一個樣本的 age 對應的 Shap 值
③ 顏色:capital_gain 越大越紅特征解釋:
① 排除所有特征的影響,描述 age 和 capital_gain 的關系。
② 年齡大的人更趨向于有大的資本收益,小部分年輕人有大的資本收益。
論文使用稱為 RETAIN 的建模策略解決了這個限制,這是一種兩級神經網絡順序數據的注意模型,提供對預測結果的詳細解釋保持與 RNN 相當的預測精度。為此,RETAIN 依賴于關注機制被建模以表示在遭遇期間醫生的行為。一個區別 RETAIN 的功能 ( 參見圖1 ) 是利用注意力生成來利用序列信息機制,同時學習可解釋的表示。并模仿醫生的行為,RETAIN 以相反的時間順序檢查患者的過去訪問,從而促進更穩定的注意后代。因此,RETAIN 會識別最有意義的訪問次數并量化訪問量有助于預測的功能。
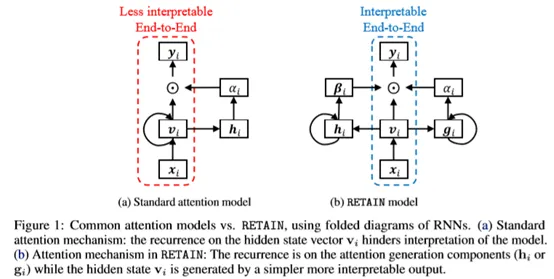
模型使用兩套權重,一套是 visit-level attention,另外一套是 variable-level attention。使用兩個 RNN 網絡分別產生。
Step1:使用線性 embedding
Step2:產生 visit-level attention。其中輸入 RNN 中的數據采用時間逆序輸入。對于稀疏的 attention,使用 Sparsemax 而不是 Softmax。
Step3:產生variable-levelattention,其中輸入 RNN 中的數據采用時間逆序輸入。
Step4:根據以上兩步生成的 attentionweight,生成 context vector。Ci 表示病人第 i 次 visit。
Step5:根據 Context Vector 生成預測結果。
逐層相關性傳播 ( LRP ) 是一種通過在神經網絡中運行反向傳遞來識別重要像素的方法。向后傳遞是保守的相關再分配過程,其中對較高層貢獻最大的神經元從其獲得最大相關性。LRP 程序如下圖所示。
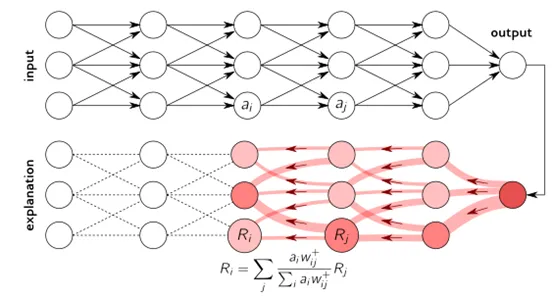
該方法可以在大多數編程語言中容易地實現并且集成到現有的神經網絡框架中。當應用于深度 ReLU 網絡時,LRP 可以被理解為預測的深度泰勒分解。
這里有如何實現 LRP 用于解釋深度模型的代碼教程,有興趣可以動手實現,用于解釋自己的深度模型。
1. Interpretable Machine Learninghttps://christophm.github.io/interpretable-ml-book/pdp.html
2. Partial dependence ——集成樹的可解析性https://zhuanlan.zhihu.com/p/40356430
3. Machine Learning for Insights Challengehttps://zhuanlan.zhihu.com/p/45898896
4. https://yyqing.me/post/2018/2018-09-25-kaggle-model-insights
5. http://rstudio-pubs-static.s3.amazonaws.com/283647_c3ab1ccee95a403ebe3d276599a85ab8.html
6. 《通向人類可理解、可解釋的人工智能》
7. https://github.com/lopusz/awesome-interpretable-machine-learning
8. https://github.com/jphall663/awesome-machine-learning-interpretability
9. https://github.com/Henrilin28/awesome-Interpretable-ML
10. http://xiangruix.com/2018/07/31/lime/
11. https://www.jianshu.com/p/b52efa66154e
12. https://zhuanlan.zhihu.com/p/32891505
13. https://suensummit.github.io/intro-lime/#1
14. https://www.oreilly.com/learning/introduction-to-local-interpretable-model-agnostic-explanations-lime
15. https://github.com/slundberg/shap
16. http://km.oa.com/group/22630/articles/show/380452?kmref=search&from_page=1&no=1
文章轉自微信公眾號@算法進階