91国内精品久久久久免费影院,日韩欧美亚洲国产一区二区三区,国产成人青草视频

二階行列式：

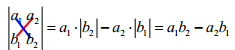
三階行列式：

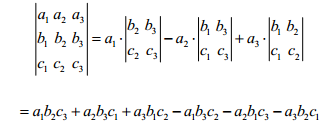
N階行列式：

這些方陣的行列式通過一系列的計(jì)算步驟得出，且每一階數(shù)的行列式計(jì)算方法都遵循其獨(dú)特的規(guī)則。

行列式的幾何意義

行列式的幾何意義可以從兩種角度理解：

二階行列式的幾何意義體現(xiàn)在它在二維平面上形成的有向面積。具體而言，一個(gè)二階行列式可以看作是平行四邊形的有向面積，其鄰邊由行向量構(gòu)成。

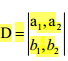
這個(gè)幾何意義的另一個(gè)解釋是：二階行列式與兩個(gè)向量的叉積等價(jià)。叉積的結(jié)果是一個(gè)向量，其大小即為該平行四邊形的面積。這一特性在物理學(xué)中用于計(jì)算力矩等物理量。

三階行列式則代表空間中的平行六面體的有向體積。這里的每一個(gè)行向量或列向量都是六面體的一條邊，行列式的值即為該六面體的體積。當(dāng)六面體的兩條鄰邊重合時(shí)，其體積為零，對應(yīng)的行列式值也為零。

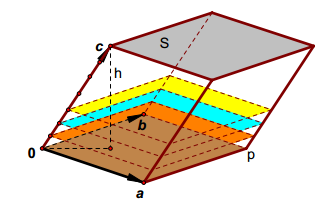
行列式的這些幾何意義不僅僅是數(shù)學(xué)概念，它們在物理、工程等領(lǐng)域的應(yīng)用中也有實(shí)際的意義。

行列式的性質(zhì)是其在數(shù)學(xué)中的應(yīng)用基礎(chǔ)。以下是行列式的一些重要性質(zhì)：

行列式的乘法性質(zhì)：

行列式的一個(gè)重要性質(zhì)是對于任意兩個(gè)方陣A和B，有：

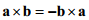
這意味著行列式在矩陣乘法下滿足交換律，即使矩陣乘法本身不滿足交互律。
行列式的交換性質(zhì)：

如果交換行列式的兩行，行列式的值會變號。這一性質(zhì)可以通過幾何直觀來理解：兩向量在同一條直線上的平行四邊形的面積為零。
行列式的對角化性質(zhì)：

行列式可以通過初等行變換化為對角形，這在計(jì)算和簡化過程中非常有用。

行列式的轉(zhuǎn)置性質(zhì)指出：矩陣A的行列式等于其轉(zhuǎn)置矩陣的行列式。這個(gè)性質(zhì)在對稱矩陣的研究中尤為重要，因?yàn)閷ΨQ矩陣的行列式具有相同的幾何意義。

行列式不僅在數(shù)學(xué)中具有理論價(jià)值，還在實(shí)際應(yīng)用中發(fā)揮著重要作用。以下是幾個(gè)行列式的實(shí)際應(yīng)用場景：

克萊姆法則是用行列式求解線性方程組的經(jīng)典方法。通過計(jì)算系數(shù)矩陣和常數(shù)項(xiàng)的行列式，可以得到方程組的解。

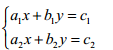
行列式在物理學(xué)中用于描述線性變換的特性。例如，在量子力學(xué)中，行列式可用于計(jì)算波函數(shù)的疊加。

行列式作為線性代數(shù)的基礎(chǔ)，在數(shù)學(xué)研究中有著豐富的課題。例如，研究行列式與特征值、特征向量之間的關(guān)系，可以深入理解矩陣的性質(zhì)。

問：行列式與矩陣有什么區(qū)別？
- 答：行列式是一個(gè)數(shù)值，而矩陣是一個(gè)數(shù)表。行列式通過矩陣的元素計(jì)算得到，代表幾何意義上的面積或體積。
問：行列式如何用于求解線性方程組？
- 答：通過克萊姆法則，行列式可以用于求解線性方程組。該方法通過計(jì)算系數(shù)矩陣和常數(shù)項(xiàng)的行列式來得到方程組的解。
問：行列式在物理中有哪些應(yīng)用？
- 答：行列式在物理學(xué)中用于描述線性變換的特性，計(jì)算力矩、量子力學(xué)中的波函數(shù)疊加等。