欧美黑人与xx,99精品国产成人一区二区,久久久综合久久

RSA的魅力在于其非對稱性，這意味著加密和解密使用的是不同的密鑰。公鑰可以公開，而私鑰必須保密。RSA算法在信息加密、安全通信和數字簽名等領域有著廣泛的應用。

RSA加密過程詳解

RSA加密過程是一個數學運算，將明文通過公鑰轉化為密文。該過程可以用一個通式來表示：

密文 = 明文^E mod N

在這個公式中，E和N構成了公鑰。要進行RSA加密，必須先生成一對密鑰對。生成公鑰和私鑰的步驟如下：

選擇兩個大質數p和q，計算N = p * q。
計算歐拉函數r = (p-1)*(q-1)。
選擇一個小于r且與r互質的整數E。
計算E關于r的模反元素，命名為D，使得E * D ≡ 1 (mod r)。
公鑰為(E, N)，私鑰為(D, N)。

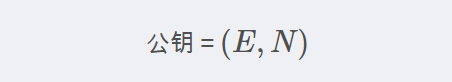
RSA加密過程

RSA解密過程

解密過程是加密過程的逆過程，使用私鑰對密文進行解密。解密算法的公式為：

明文 = 密文^D mod N

其中，D為解密密鑰。解密時，只有擁有私鑰的人才能將密文轉換回明文。這種加密和解密的互逆性使得RSA算法在信息安全領域具有極高的實用價值。

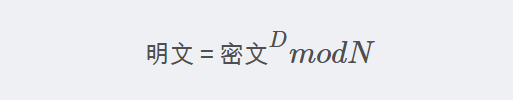
RSA解密過程

生成密鑰對的詳細步驟

生成RSA密鑰對的過程涉及復雜的數學計算，下面是一個詳細的步驟描述：

生成質數p和q

選擇兩個大質數p和q是生成RSA密鑰對的第一步。這兩個數的選擇直接影響密鑰的安全性。因此，質數不能太小，否則容易被破解。通常使用概率算法來驗證大整數是否為質數。

計算N和歐拉函數r

一旦選擇了質數p和q，計算N = p q。接著，計算歐拉函數r = (p-1) (q-1)，這一步是為了后續生成公鑰和私鑰做準備。

選擇公鑰指數E

E必須滿足兩個條件：1 < E < r，并且E與r互質。一般選擇65537作為E，因為它是一個常用的公鑰指數，能在保證安全的同時提高計算效率。

計算私鑰指數D

私鑰指數D是通過求解以下模反元素方程得到的：

E * D ≡ 1 (mod r)

D的計算可以通過擴展歐幾里得算法來實現。

銷毀質數p和q

完成密鑰對的生成后，必須安全銷毀質數p和q，以防止私鑰被推導出來。

實踐中的RSA加解密示例

為了更好地理解RSA加密算法，我們可以通過一個簡單的例子來演示：

假設選擇質數p = 17和q = 19，則：

計算N = 17 * 19 = 323。
計算r = (17-1)*(19-1) = 288。
選擇E = 5，因為5與288互質。
計算D，使得5 * D ≡ 1 (mod 288)。通過計算可得D = 173。

公鑰為(5, 323)，私鑰為(173, 323)。

加密過程

假設明文是123，使用公鑰加密：

密文 = 123^5 mod 323 = 240

解密過程

使用私鑰解密密文：

明文 = 240^173 mod 323 = 123

Java中RSA加解密的注意事項

在Java中實現RSA加解密時，有一些重要的注意事項需要考慮：

質數的選擇

選擇合適的質數對RSA算法的安全性至關重要。應使用可靠的算法生成大質數，并確保隨機數生成器的安全性。

密鑰長度的影響

密鑰長度直接影響加密強度和計算效率。雖然較長的密鑰更安全，但也會降低加解密速度。通常，1024位或2048位是比較常見的選擇。

加密數據長度限制

RSA加密的數據長度不能超過密鑰長度減去11字節。因此，較長的數據需要使用分塊加密或結合對稱加密算法。

Java中實現示例

以下是Java中實現RSA加解密的簡單示例：

import java.security.*;
import javax.crypto.Cipher;

public class RSADemo {
    public static void main(String[] args) throws Exception {
        KeyPairGenerator keyGen = KeyPairGenerator.getInstance("RSA");
        keyGen.initialize(2048);
        KeyPair pair = keyGen.generateKeyPair();
        PublicKey publicKey = pair.getPublic();
        PrivateKey privateKey = pair.getPrivate();

        Cipher cipher = Cipher.getInstance("RSA");

        // Encrypt
        cipher.init(Cipher.ENCRYPT_MODE, publicKey);
        byte[] encryptedData = cipher.doFinal("Hello, RSA!".getBytes());

        // Decrypt
        cipher.init(Cipher.DECRYPT_MODE, privateKey);
        byte[] decryptedData = cipher.doFinal(encryptedData);

        System.out.println("Decrypted: " + new String(decryptedData));
    }
}