
Google語音識別技術詳解與實踐應用
羅巴切夫斯基、波爾約和高斯的故事,展現了非歐幾何學創立過程中數學家的堅持與勇氣。他們不僅對真理的執著追求震撼人心,而且對新幾何的邏輯相容性抱有信心,相信這與歐幾里得幾何一樣正確。
非歐幾何學的創立基于邏輯上互不矛盾的一組假設,這一發現表明,不同的幾何學可以共存,為數學提供了更廣闊的發展空間。
非歐幾何學不僅擴大了幾何學的研究對象,還促進了數學分支的發展,如數的概念、分析基礎、數學基礎和數理邏輯等。它還引發了對數學本質的深入探討,改變了人們對時間和空間的物理觀念。
愛因斯坦的廣義相對論是宇宙結構幾何學的一個最佳論證,它采用了非歐幾何學的概念來描述時空的彎曲。這一理論的提出,進一步證實了非歐幾何學在現代物理學中的重要性。
非歐幾何學的概念也被應用于醫學、地球科學等多個領域,為解決實際問題提供了新的視角和方法。
歐氏幾何、羅氏幾何和黎曼幾何雖然基于不同的假設,但它們各自構成了一個嚴密的公理體系,適用于不同的空間和情境。
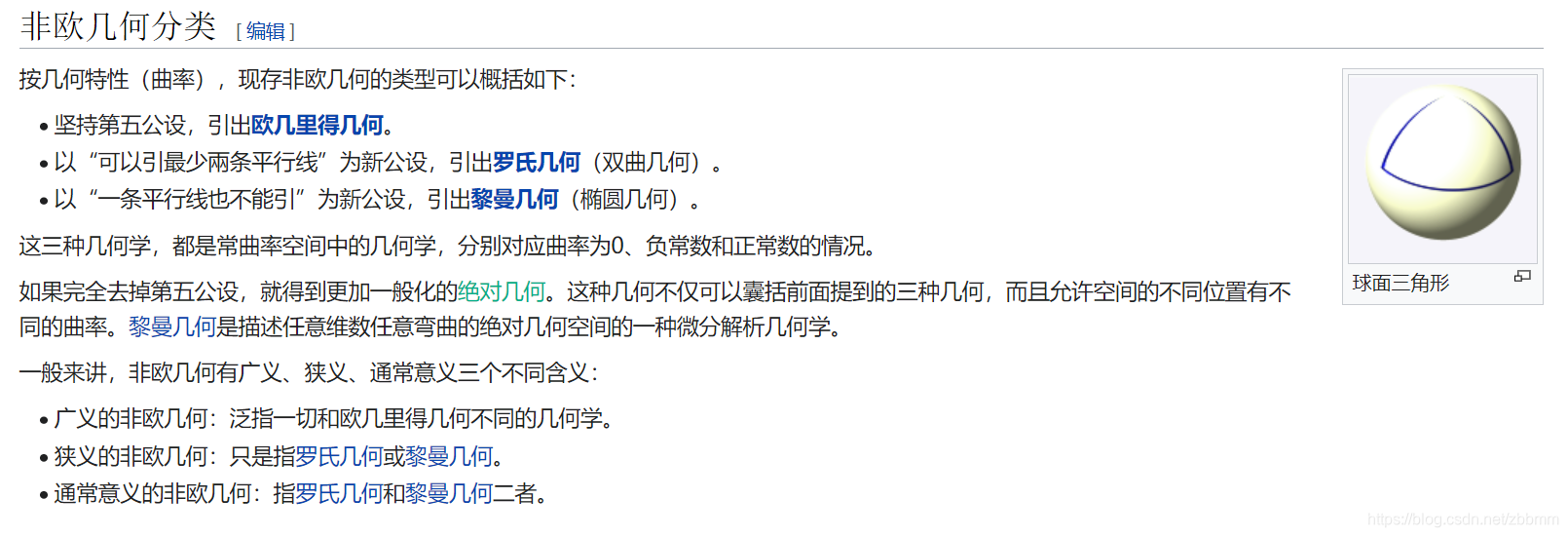
在我們的日常生活中,歐式幾何是最常用的幾何學,它適用于描述平面上的形狀和距離。
羅氏幾何適用于描述具有負曲率的空間,如馬鞍面,它在宇宙空間和原子核世界中更為適用。
黎曼幾何適用于描述具有正曲率的空間,如球面,它在地球表面研究航海、航空等實際問題中有著廣泛的應用。
非歐幾何學的創立不僅打破了兩千多年來歐式幾何一統天下的局面,還從根本上改變了人們的幾何觀。這一變革對數學、自然科學乃至哲學的發展都產生了深遠的影響。
非歐幾何學的出現,使數學哲學研究進入了一個嶄新的時期。它證明了幾何學公設并非先驗綜合判斷,而是可以被選擇和改變的約定俗成的慣例。
非歐幾何學的發展表明,數學不再是客觀世界的直接反映,而是客觀世界的模型。我們可以根據需要選擇不同的模型來描述和理解世界。
問:非歐幾何學是如何誕生的?
問:非歐幾何學在現代科學中有哪些應用?
問:歐氏幾何、羅氏幾何和黎曼幾何有何不同?
問:非歐幾何學對數學哲學有何影響?
問:我們如何選擇使用哪種幾何學?