精品无人区乱码1区2区3区在线,国产成人免费视频,亚洲午夜在线播放

極大似然原理

極大似然原理是概率論在統(tǒng)計學(xué)中的應(yīng)用，核心思想是通過對已發(fā)生事件概率的最大化來進(jìn)行參數(shù)估計。在一個隨機試驗中，許多事件都有可能發(fā)生，概率大的事件發(fā)生的概率也大。因此，當(dāng)某一事件發(fā)生，我們有理由認(rèn)為該事件的發(fā)生概率比其他事件要大。

例如，假設(shè)一個箱子里有紅色和黑色兩種顏色的球，數(shù)量分別為10個和1個。我們并不知道哪種顏色的球為10個，這時我們隨機從箱子里拿出一個球，如果這個球是紅色的，我們就認(rèn)為盒子里紅球有10個，黑球有1個。

極大似然估計概述

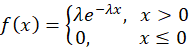
極大似然估計（Maximum Likelihood Estimation, MLE）是一種統(tǒng)計推斷方法，旨在通過給定的數(shù)據(jù)找到使觀測數(shù)據(jù)出現(xiàn)概率最大的參數(shù)值。極大似然估計法由高斯和費希爾先后提出，是被使用最廣泛的一種參數(shù)估計方法，基于直觀的極大似然原理。

極大似然估計的基本思想

極大似然估計的基本思想是利用已知的樣本結(jié)果信息，反推最有可能導(dǎo)致這些樣本結(jié)果出現(xiàn)的模型參數(shù)值。換句話說，極大似然估計提供了一種給定觀察數(shù)據(jù)來評估模型參數(shù)的方法，即：“模型已定，參數(shù)未知”。通過若干次試驗，觀察結(jié)果，利用試驗結(jié)果得到某個參數(shù)值能夠使樣本出現(xiàn)的概率為最大。

似然函數(shù)與其構(gòu)建

似然函數(shù)是一種關(guān)于統(tǒng)計模型中參數(shù)的函數(shù)，表示模型參數(shù)中的似然性，用 L 表示。給定輸出 x 時，關(guān)于參數(shù) θ 的似然函數(shù) L(θ|x) 在數(shù)值上等于給定參數(shù) θ 后變量 x 的概率。

似然函數(shù)的定義

似然性（likelihood）與概率（possibility）同樣可以表示事件發(fā)生的可能性大小，但是二者有著很大的區(qū)別：

概率 p(x|θ) 是在已知參數(shù) θ 的情況下，發(fā)生觀測結(jié)果 x 的可能性大小。
似然性 L(θ|x) 則是從觀測結(jié)果 x 出發(fā)，推斷分布函數(shù)的參數(shù) θ 的可能性大小。

最大似然估計的應(yīng)用案例

例子：球的顏色估計

假設(shè)有一個罐子，里面有黑白兩種顏色的球，數(shù)目多少不知。我們想知道罐中白球和黑球的比例，但不能把罐中的球全部拿出來數(shù)。我們可以通過抽樣來估計罐中黑白球的比例。假如在一百次抽樣中，有七十次是白球，請問罐中白球所占的比例最有可能是多少？

通過極大似然估計，我們可以假設(shè)罐中白球的比例是 p，那么黑球的比例就是 1-p。因此，我們可以通過概率計算得出白球的比例。

例子：全國人民年均收入的估計

假設(shè)我們要統(tǒng)計全國人民的年均收入，收入服從正態(tài)分布，但該分布的均值與方差未知。我們可以選取一個城市或鄉(xiāng)鎮(zhèn)的人口收入，作為我們的觀察樣本結(jié)果。通過最大似然估計來獲取正態(tài)分布的參數(shù)。

最大似然估計的優(yōu)缺點

優(yōu)點

高效性：在一定條件下，最大似然估計是漸近無偏的，即樣本足夠大時估計值逼近真值。
普適性：適用于多種類型數(shù)據(jù)和模型，靈活性強。

缺點

計算復(fù)雜：對于某些復(fù)雜模型，似然函數(shù)難以求解，計算量大。
依賴樣本：估計的準(zhǔn)確性依賴于樣本量和樣本質(zhì)量。樣本量不足時，可能產(chǎn)生偏差。

最大似然估計與其他估計方法比較

與最小二乘法比較

最小二乘法主要用于線性回歸模型，而最大似然估計適用于更廣泛的統(tǒng)計模型。兩者在處理誤差分布假設(shè)上有所不同，最小二乘法假設(shè)誤差為正態(tài)分布，而最大似然估計不受此限制。

與貝葉斯估計比較

貝葉斯估計利用先驗分布和觀測數(shù)據(jù)進(jìn)行參數(shù)估計，而最大似然估計僅依賴于觀測數(shù)據(jù)。貝葉斯估計能處理參數(shù)的不確定性，但計算復(fù)雜度較高。

實際應(yīng)用中的最大似然估計

最大似然估計在機器學(xué)習(xí)、經(jīng)濟(jì)學(xué)、生物統(tǒng)計學(xué)等領(lǐng)域有廣泛應(yīng)用。例如，在機器學(xué)習(xí)中用于模型參數(shù)的優(yōu)化；在經(jīng)濟(jì)學(xué)中用于市場分析和定價模型的參數(shù)估計；在生物統(tǒng)計學(xué)中用于基因組數(shù)據(jù)的分析。

FAQ

問：最大似然估計與貝葉斯估計有什么區(qū)別？
- 答：最大似然估計僅依賴于觀測數(shù)據(jù)，而貝葉斯估計結(jié)合先驗分布和觀測數(shù)據(jù)來進(jìn)行參數(shù)估計。
問：在什么情況下使用最大似然估計？
- 答：最大似然估計適用于需要估計參數(shù)的各種統(tǒng)計模型，尤其是在樣本量較大且數(shù)據(jù)獨立同分布時效果最佳。
問：最大似然估計是否總是無偏的？
- 答：不是，最大似然估計在樣本量不足時可能產(chǎn)生偏差，但在樣本量足夠大時，漸近無偏。
問：最大似然估計如何處理多參數(shù)模型？
- 答：最大似然估計可以通過多維優(yōu)化技術(shù)，如梯度下降法，來求解多參數(shù)模型的最優(yōu)參數(shù)。
問：最大似然估計的計算復(fù)雜度如何？
- 答：計算復(fù)雜度取決于模型的復(fù)雜度和參數(shù)的數(shù)量，對于復(fù)雜模型，計算復(fù)雜度較高。