全網最詳細的Spring入門教程
并積轉置通過學習可調整的參數，能夠在神經網絡中自動尋找最佳的上采樣方式，超越了傳統插值方法（如雙線性插值和雙立方插值）帶來的局限性。
并積轉置廣泛應用于需要高精度重構的場景中，例如：
生成對抗網絡（GAN）：在生成對抗網絡中，生成器通過并積轉置將噪聲向量轉換為高分辨率圖像。
語義分割：在語義分割任務中，網絡需要將低分辨率的特征圖還原到原始圖像大小，以便逐像素進行分類。這一過程在U-Net和FCN等網絡架構中廣泛應用。
圖像超分辨率：通過并積轉置可以從低分辨率的圖像生成高分辨率的版本，提升圖像細節。
普通卷積通過對輸入特征圖施加卷積核進行特征提取，通常實現從大尺寸到小尺寸的降采樣。其操作本質上是多對一的映射，意味著多個輸入特征映射到一個輸出特征。
并積轉置則反其道而行之，通過將卷積核反向應用，達到將一個輸入特征擴展為多個輸出特征的效果，從而實現圖像的上采樣。
為了理解并積轉置的運作原理，我們可以從數學上推導其計算過程。假設有一個輸入矩陣和一個卷積核，普通卷積將輸入矩陣展平為一列向量，與卷積核的轉換矩陣進行矩陣乘法，得出輸出。
而在并積轉置中，我們將其逆向操作：轉換矩陣的轉置與輸出向量相乘，恢復成輸入矩陣的形狀。這種逆向計算體現了一對多的映射關系。
圖2 轉置后卷積矩陣運算示例
并積轉置的輸出大小可以通過步長、填充和卷積核大小等參數來控制。
當步長為1時，并積轉置的輸出大小等于輸入大小加上卷積核大小減1。這相當于在輸入元素之間插入零值，然后應用普通卷積。
當步長大于1時，并積轉置的輸出會更加復雜。為了達到期望的輸出尺寸，常需要在輸入矩陣中插入更多的零值，并調整填充量以匹配輸出形狀。
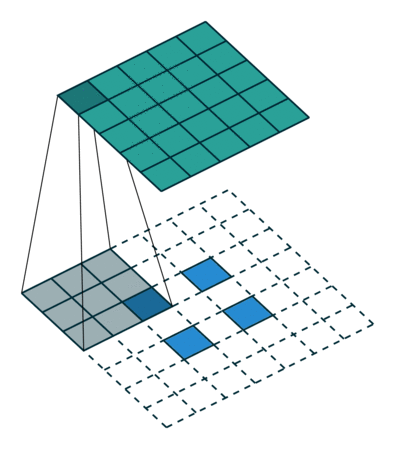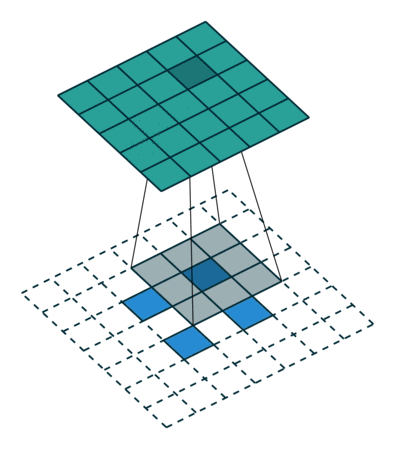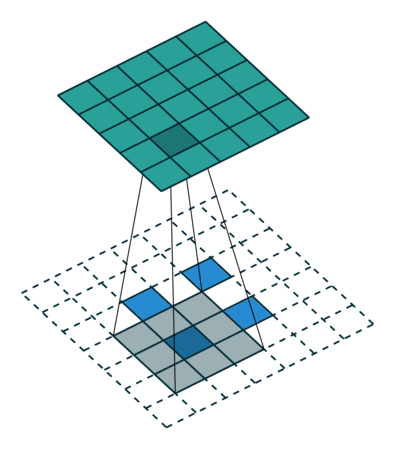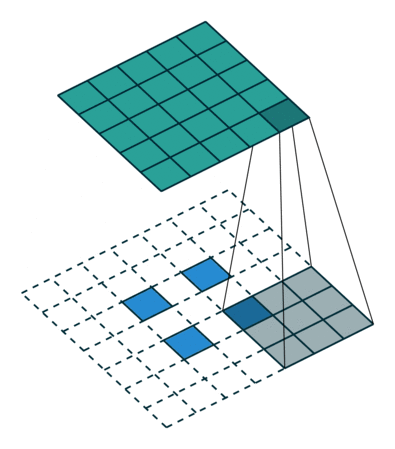圖3 s=2 時，轉置卷積運算示例
并積轉置是深度學習中用于上采樣的一種重要技術。它通過可學習的參數，提供了一種靈活的方式來恢復圖像尺寸，并在圖像生成和語義分割等領域得到廣泛應用。然而，使用時需注意其可能帶來的棋盤效應，并借助改進的方法進行優化。
問：并積轉置和反卷積是同一種操作嗎？
問：為什么并積轉置會引起棋盤效應？
問：并積轉置在GAN中如何應用？
通過對并積轉置的深入理解，我們可以在深度學習中更加高效地進行圖像處理，提升模型的性能與效果。
