角度與圓

• ∠ 表示角度，用來量度兩條射線之間的夾角大小。
• ⊙ 表示圓，用來描述所有與給定點（圓心）距離相等的點的集合。

三角形與全等

• △ 表示三角形，是幾何中最基本的多邊形。
• ≡ 表示全等，用來說明兩個幾何圖形在形狀和大小上的一致性。

代數符號詳述

代數符號在數學中用來表示未知量、方程和不等式等概念。以下是一些關鍵的代數符號及其含義：

未知量與計算

• ∝ 表示成正比，用來描述兩個量之間的線性關系。
• ∨ 和 ∧ 分別表示邏輯或和邏輯與，常用于描述復雜的條件語句。

不等式與無限

• ∞ 表示無窮大，用來描述趨向于無限大的趨勢或者數量。
• ≈ 表示近似等于，用來表達兩個數值在一定誤差范圍內的接近程度。

運算符號的實際應用

運算符號是進行數學計算的基礎，它們定義了基本的數學操作。以下是一些基本的運算符號及其應用：

加法與減法

• + 和 – 分別表示加法和減法，是最基本的算術運算。

例：

5 + 3 = 8

10 - 4 = 6

乘法與除法

• × 和 ÷ 分別表示乘法和除法，用于計算兩個數的乘積和商。

例：

8 × 2 = 16

20 ÷ 4 = 5

集合符號的重要性

集合論是數學的基礎分支之一，集合符號在描述集合的關系和運算中起著核心作用。以下是一些基本的集合符號及其含義：

并集與交集

• ∪ 表示兩個集合的并集，包含所有屬于任一集合的元素。
• ∩ 表示兩個集合的交集，包含同時屬于兩個集合的元素。

屬于與包含

• ∈ 表示屬于，用來說明某個元素是某個集合的成員。
• ? 和 ? 表示子集關系，用來描述集合之間的包含關系。

數學符號的邏輯推理

邏輯推理是數學證明中不可或缺的一部分，以下是一些基本的推理符號及其含義：

蘊含與等價

• ? 表示蘊含，用來說明如果條件A成立，則條件B也成立。
• ? 表示等價，用來說明兩個命題的真假情況完全相同。

否定與合取

• ? 表示否定，用來表達命題的對立面。
• ∧ 表示合取，用來連接多個命題，只有當所有命題都為真時，合取命題才為真。

數學符號在微積分中的應用

微積分是研究變化率和累積量的數學分支，以下是一些微積分中常用的符號及其應用：

導數與積分

• dx 表示微分，用來描述函數在某一點的變化率。
• ∫ 表示積分，用來計算函數在某個區間的累積量。

基本初等函數求導公式

微分方程

微分方程是描述函數與其導數之間關系的方程，廣泛應用于物理學和工程學中。

FAQ

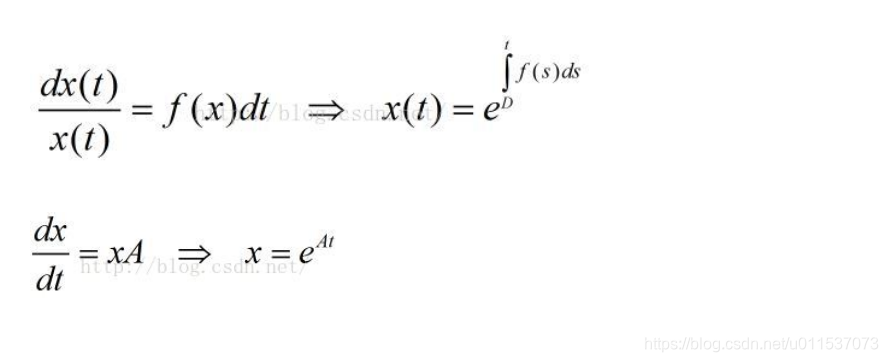
1. 問：數學符號有哪些主要類別？
   答：數學符號主要分為幾何符號、代數符號、運算符號、集合符號和推理符號等類別。

2. 問：集合符號中的并集和交集有什么區別？
   答：并集包含兩個集合中所有的元素，而交集只包含兩個集合共有的元素。

3. 問：微積分中的導數和積分分別表示什么？
   答：導數表示函數在某一點的變化率，積分表示函數在某個區間的累積量。

4. 問：如何理解邏輯推理中的蘊含和等價？
   答：蘊含表示如果一個命題為真，則另一個命題也必須為真；等價表示兩個命題在邏輯上是等價的，即它們具有相同的真值。

5. 問：微分方程在實際問題中有哪些應用？
   答：微分方程在物理學、工程學等領域中有著廣泛的應用，如描述物體的運動、信號的傳播等。

#你可能也喜歡這些API文章!

AI聊天無敏感詞：技術原理與應用實踐

理解Webhook：它是什么以及與API的區別

自然語言處理（NLP）中的BERT與LSTM：結合應用與實踐

PPO算法深度解析與應用實踐

墨跡天氣應用與API集成實踐

Node.js 后端開發指南：搭建、優化與部署

Java 文件加密與傳輸：全面指南

實時語音翻譯軟件全面解析與推薦

Optuna使用詳解與案例分析