數據庫表關聯：構建高效數據結構的關鍵
泰勒公式是麥克勞林公式的推廣，它不局限于 (x_0=0)，而是在 (x_0) 處展開。其形式為：
[ f(x) = f(x_0) + f'(x_0)(x-x_0) + frac{f”(x_0)}{2!}(x-x_0)^2 + cdots ]
泰勒公式在工程學和物理學中具有重要的應用價值。
在統計學中，冪處常用于擬合數據分布。尤其在處理大數據或復雜數據集時，冪律分布（power-law distribution）是一種常用模型。
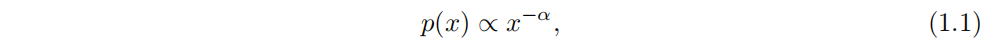
冪律分布有連續(xù)和離散兩種基本形式。連續(xù)冪律分布由概率密度 (p(x)) 描述，而離散冪律分布則關注于量只能取一組離散值的情況。
在處理冪律分布時，極大似然估計法是常用的參數化方法。此方法可以有效估計尺度參數 (alpha) 和數據的冪律行為的下界。
隨著科學和工程技術的發(fā)展，冪處在數學、物理、工程和數據科學等領域中的應用將變得更加廣泛。未來的研究可能集中在提高冪級數的計算效率、優(yōu)化其在大數據分析中的應用等。
冪處作為數學分析中的一個基本工具，其廣泛的應用和重要的性質使其成為數學研究和應用中的一個重要領域。通過對冪處的深入理解，我們可以更好地解決復雜的數學問題，提升科學研究的深度和廣度。
問：什么是冪處？
問：冪處有哪些應用？
問：如何判斷一個函數能否展開成冪處？
問：什么是冪律分布？
問：泰勒公式與麥克勞林公式有何區(qū)別？
