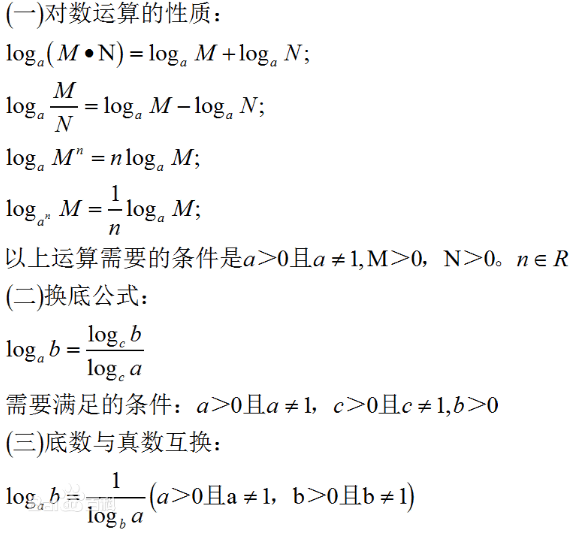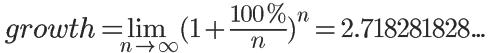對數函數的性質
對數函數是指形如 $y = log_a x$ 的函數,其中 $x$ 是自變量。對數函數具有以下基本性質:
函數的定義域
對數函數的定義域為所有正實數,即 $x > 0$。這是因為對數僅對正數有意義,負數和零沒有對數。
函數的基本性質
- 過定點:當 $x = 1$ 時,$y = log_a 1 = 0$。
- 單調性:
- 當 $a > 1$ 時,$log_a x$ 是增函數。
- 當 $0 < a < 1$ 時,$log_a x$ 是減函數。

對數運算法則
對數的運算遵循幾條重要的法則,這些法則與指數運算密切相關:
積的對數
兩個正數的積的對數等于它們對數的和:
$$ log_a (MN) = log_a M + log_a N $$
商的對數
兩個正數商的對數等于它們對數的差:
$$ log_a left( frac{M}{N} right) = log_a M – log_a N $$
冪的對數
一個正數冪的對數等于冪的指數乘以底數的對數:
$$ log_a (M^p) = p cdot log_a M $$

對數公式的推導
對數公式的推導是理解對數運算的關鍵。以下是常見對數恒等式及其證明:
恒等式
對于 $a^t = N$,其中 $a > 0$ 且 $a neq 1$,有恒等式:
$$ a^{log_a N} = N $$
證明
設 $log_a N = t$,則 $a^t = N$,從而有 $a^{log_a N} = a^t = N$,證明完畢。
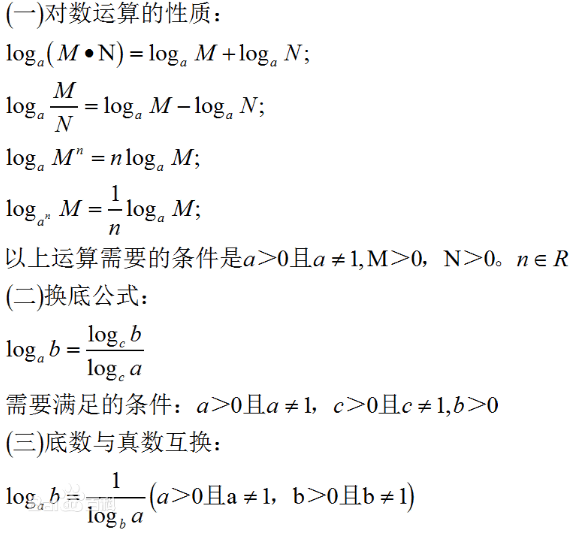
對數的實際應用
在實際應用中,對數具有廣泛的應用場景,包括科學計算、工程領域、金融分析等。以下是對數在一些實際場景中的應用:
科學計算中的應用
對數在科學計算中常用于處理指數增長的現象,例如細胞分裂、放射性衰變等。自然對數 $e$ 作為增長率的極限值,在描述連續增長過程時尤為重要。
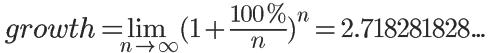
金融領域中的應用
在金融領域,對數常用于計算復利、評估股票增長率等。對數能夠簡化復雜的指數計算,使得金融分析更為直觀。
對數的誤區與注意事項
雖然對數在數學中是一個強有力的工具,但在使用過程中仍需注意一些常見誤區:
負數與零無對數
在實數范圍內,負數和零沒有對數。這是因為對數函數的定義域僅限于正數。
虛數范圍內的對數
在虛數范圍內,負數是有對數的,但這涉及到復數對數的概念,與實數對數不同。
代碼示例:對數運算實現
為了更好地理解對數的運算,我們可以通過編程來實現對數運算的基本規則。
import math
def log_operations(base, number):
# 計算對數
log_value = math.log(number, base)
return log_value
result = log_operations(10, 100)
print(f"log_10(100) = {result}")
FAQ
什么是對數?
對數是指數函數的反函數,用于表示一個數是底數的多少次冪。
對數有什么實際應用?
對數在科學計算、金融分析和工程領域中有廣泛應用,常用于處理指數增長問題。
為什么負數沒有對數?
在實數范圍內,負數沒有對數,因為對數函數的定義域僅限于正數。
什么是自然對數?
自然對數是以無理數 e 為底的對數,常用于描述自然界中的連續增長現象。
如何計算對數運算?
對數運算可以通過積、商、冪的對數公式進行計算,也可以使用編程語言中的對數函數實現。
熱門推薦
一個賬號試用1000+ API
助力AI無縫鏈接物理世界 · 無需多次注冊
3000+提示詞助力AI大模型
和專業工程師共享工作效率翻倍的秘密
国内精品久久久久影院日本,日本中文字幕视频,99久久精品99999久久,又粗又大又黄又硬又爽毛片
亚洲午夜视频在线观看|
日韩视频一区在线观看|
日韩精品亚洲一区|
一区二区三区在线观看网站|
自拍偷拍欧美激情|
一区二区三区鲁丝不卡|
一区二区三区高清|
亚洲成av人影院在线观看网|
日本美女视频一区二区|
美女视频黄频大全不卡视频在线播放|
日日夜夜精品视频免费|
日韩av中文在线观看|
久久精品国产精品青草|
国产成人高清在线|
97久久超碰国产精品|
在线一区二区观看|
欧美一区二区视频在线观看
|
欧美精彩视频一区二区三区|
国产欧美一区二区精品性色
|
欧美激情一区二区三区全黄|
中文字幕色av一区二区三区|
一区二区三区四区在线免费观看|
在线观看日韩电影|
精品免费日韩av|
欧美三区在线视频|
日本韩国精品在线|
蜜臀久久99精品久久久久宅男|
蜜乳av一区二区|
国产一区二区免费视频|
波多野结衣中文一区|
91视频免费观看|
日韩一级黄色片|
国产精品成人一区二区艾草|
国产女同互慰高潮91漫画|
欧美一区二区成人|
久久久国产精华|
亚洲男人的天堂在线观看|
日韩电影在线免费|
jizz一区二区|
欧美mv日韩mv国产网站app|
国产精品久久一级|
日本不卡一区二区三区高清视频|
国产精选一区二区三区|
欧美日韩一区二区三区在线|
中文字幕av不卡|
蜜臀av一区二区在线免费观看|
成人av电影免费观看|
日韩一区二区在线观看视频|
亚洲色欲色欲www|
精品在线播放免费|
欧美日韩另类国产亚洲欧美一级|
国产精品免费视频网站|
乱中年女人伦av一区二区|
欧美自拍偷拍一区|
国产精品国产自产拍高清av王其|
男人的天堂久久精品|
在线观看视频一区|
亚洲婷婷在线视频|
国产99久久久国产精品|
日韩精品在线一区二区|
性久久久久久久久|
欧洲国内综合视频|
依依成人综合视频|
懂色av一区二区在线播放|
精品国产乱码久久久久久久久|
香蕉成人啪国产精品视频综合网|
色狠狠色噜噜噜综合网|
中文字幕佐山爱一区二区免费|
国产一区免费电影|
欧美精品一区二区久久久|
蜜桃av一区二区|
欧美一区二区三区电影|
日韩专区在线视频|
9191久久久久久久久久久|
亚洲成av人片一区二区梦乃
|
在线区一区二视频|
中文字幕视频一区|
91亚洲资源网|
亚洲美女在线国产|
色婷婷综合久久久中文一区二区|
中文字幕一区二区三区四区不卡|
99久久精品国产一区二区三区|
国产精品乱人伦|
91免费视频网|
亚洲一区二区三区四区中文字幕|
欧美亚洲一区二区三区四区|
亚洲图片欧美色图|
欧美一级在线视频|
国产一区二区三区高清播放|
久久久不卡网国产精品一区|
成人久久18免费网站麻豆|
中文字幕国产一区二区|
91一区一区三区|
亚洲高清不卡在线观看|
欧美一区日韩一区|
国产一区不卡在线|
1000部国产精品成人观看|
色999日韩国产欧美一区二区|
亚洲一区在线看|
欧美一级久久久|
国产69精品久久99不卡|
综合激情网...|
这里只有精品99re|
国产精品18久久久久久久久|
国产精品成人免费|
欧美日韩成人综合天天影院
|
日韩一区二区三区电影|
国产suv一区二区三区88区|
国产精品欧美一区二区三区|
欧美无人高清视频在线观看|
美女视频网站黄色亚洲|
国产精品看片你懂得|
欧美男同性恋视频网站|
国内精品写真在线观看|
亚洲免费毛片网站|
26uuu精品一区二区三区四区在线
26uuu精品一区二区在线观看
|
顶级嫩模精品视频在线看|
亚洲精品菠萝久久久久久久|
欧美成人欧美edvon|
一本一道久久a久久精品综合蜜臀|
青青草国产成人99久久|
1区2区3区欧美|
精品国产91乱码一区二区三区|
99久久综合国产精品|
免费观看一级特黄欧美大片|
国产精品久久久久久福利一牛影视
|
中文字幕第一页久久|
91精品福利在线一区二区三区|
国产91色综合久久免费分享|
日本午夜一本久久久综合|
亚洲欧美一区二区三区极速播放
|
国产白丝网站精品污在线入口|
偷拍与自拍一区|
亚洲欧美国产三级|
久久色成人在线|
在线播放一区二区三区|
色综合欧美在线视频区|
国产成人免费视频一区|
爽好多水快深点欧美视频|
亚洲六月丁香色婷婷综合久久
|
日本韩国一区二区三区视频|
国产剧情一区二区三区|
麻豆精品国产传媒mv男同|
亚洲在线视频免费观看|
亚洲人午夜精品天堂一二香蕉|
久久综合九色综合久久久精品综合
|
夫妻av一区二区|
国模无码大尺度一区二区三区|
日韩国产在线观看|
午夜精品影院在线观看|
亚洲一级二级在线|
亚洲制服丝袜在线|
亚洲亚洲精品在线观看|
一区二区在线免费观看|
亚洲免费看黄网站|
亚洲同性gay激情无套|
中文字幕一区二区三区在线不卡|
欧美激情一区不卡|
久久久精品国产免大香伊|
久久夜色精品国产噜噜av|
精品国产乱子伦一区|
亚洲精品在线观看网站|
久久久五月婷婷|
日本一区二区三区电影|
国产午夜精品久久久久久免费视
|
蜜臀av性久久久久蜜臀aⅴ四虎
|
日韩av二区在线播放|
男男成人高潮片免费网站|
免费观看91视频大全|
午夜久久久影院|
麻豆国产精品官网|
国产精品自拍毛片|
成人国产一区二区三区精品|
91免费观看国产|
欧美丰满美乳xxx高潮www|
日韩欧美一区二区三区在线|
久久精品一区二区三区不卡牛牛
|
中文字幕中文字幕在线一区|
亚洲欧美一区二区三区久本道91|
一区二区三区在线观看视频|
五月天一区二区三区|
久久成人av少妇免费|
菠萝蜜视频在线观看一区|
欧美天堂亚洲电影院在线播放|
51午夜精品国产|
久久精品夜色噜噜亚洲aⅴ|
亚洲三级电影网站|
秋霞成人午夜伦在线观看|
国产精品1024|
在线观看免费视频综合|
欧美一区二区视频在线观看2022|
久久精品一区二区三区不卡牛牛|
亚洲三级理论片|
老司机精品视频线观看86|
成人免费av网站|
7777精品伊人久久久大香线蕉经典版下载
|
一区在线观看免费|
麻豆成人av在线|
在线中文字幕不卡|
国产亚洲污的网站|