
大模型RAG技術:從入門到實踐
在天體力學中,拉格朗日點是限制性三體問題的五個特解。歐拉和拉格朗日通過研究二體系統的引力場推算出了這些點的位置:L1、L2、L3由歐拉推算出,而L4和L5則是由拉格朗日推算的。
以下是計算拉格朗日點位置的偽代碼示例:
import math
def calculate_lagrange_points(m1, m2, distance):
# m1和m2為兩個天體的質量,distance為兩者之間的距離
L1 = distance * (1 - (m2 / (3 * m1))**(1/3))
L2 = distance * (1 + (m2 / (3 * m1))**(1/3))
L3 = distance * (1 + 5 * (m2 / (12 * m1)))
return L1, L2, L3在行星和恒星系統中,常見的拉格朗日點有五個:L1、L2、L3、L4和L5。L1、L2和L3位于兩大天體的連線上,而L4和L5則位于公轉軌道的60度位置。

L1位于兩大天體之間,是進行太陽觀測的理想位置,如SOHO和深空氣象衛星就位于此。L2則位于背向太陽的地球方向,適合深空觀測,詹姆斯·韋伯太空望遠鏡將被部署在此進行宇宙紅外輻射觀測。L3雖然在科幻小說中常被提及,但在現實中尚未被實際利用。
L4和L5在公轉軌道上的60度位置上形成等邊三角形,因其穩定性,被認為是可能的太空殖民區域。木星的特洛伊小行星群也聚集在L4和L5周圍。
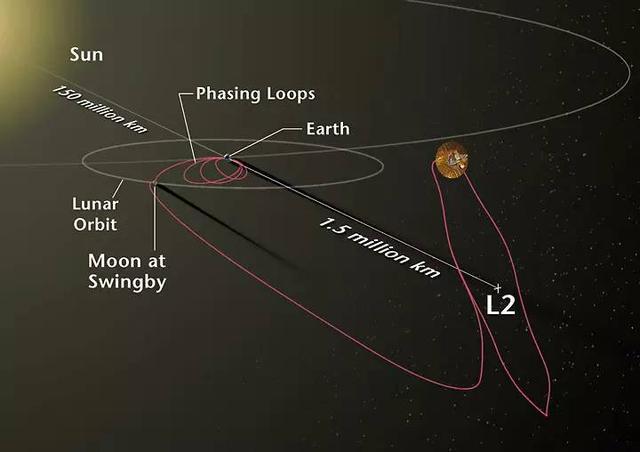
拉格朗日點為科學研究提供了穩定的觀測平臺。L1和L2點特別適合安裝天文望遠鏡和探測器,如SOHO和WMAP。
由于拉格朗日點的獨特位置,許多太空任務選擇這些點作為探測器的駐留位置。詹姆斯·韋伯太空望遠鏡將利用L2點來減少地球和太陽的光干擾,從而更有效地進行深空探測。
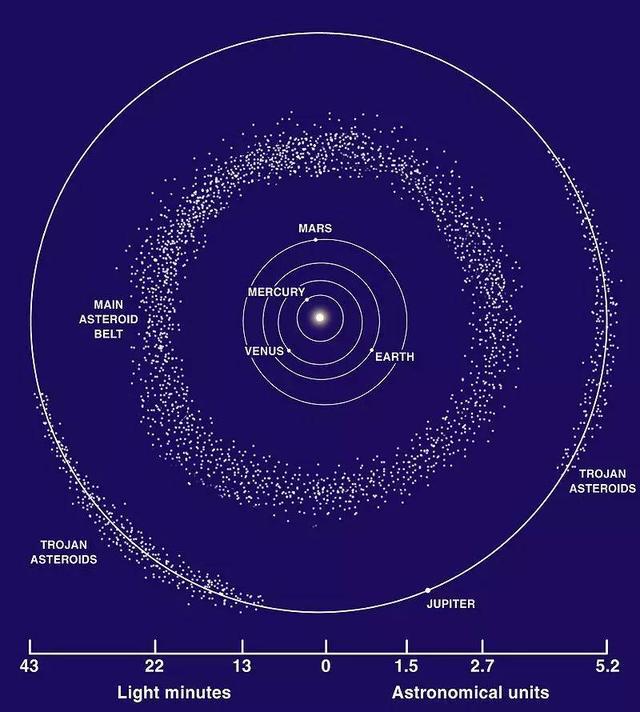
拉格朗日點提供了一個穩定的環境,適合未來太空殖民的研究。L4和L5因其穩定性,被認為是可能的太空殖民地。
在這些點上,技術挑戰包括保持軌道穩定性和進行有效的通訊。使用微調和軌道修正技術可以幫助解決這些問題。
拉格朗日點為現代天文學和航天任務提供了無可比擬的優勢。無論是在觀測太陽系外的深空,還是作為未來太空殖民的前哨基地,拉格朗日點都具有巨大的潛力。
問:什么是拉格朗日點?
問:L2點的主要用途是什么?
問:為什么L4和L5點被認為是太空殖民的潛在地點?
問:在拉格朗日點上部署探測器有哪些挑戰?
問:L3點在現實中有應用嗎?