国产精品久久亚洲一区二区,乱一色一一区二区三区,亚洲午夜顶级嘿嘿嘿影院

1. 拉格朗日乘數(shù)法的基本概念

1.1 什么是拉格朗日乘數(shù)法？

拉格朗日乘數(shù)法是一種在數(shù)學(xué)優(yōu)化問題中用于尋找條件極值的方法。它通過引入拉格朗日乘子，將原本受限的問題轉(zhuǎn)化為無約束優(yōu)化問題，從而簡化求解過程。這種方法廣泛應(yīng)用于多元函數(shù)的極值問題，特別是在經(jīng)濟學(xué)和工程學(xué)中具有重要意義。

1.2 關(guān)鍵術(shù)語與定義

在拉格朗日乘數(shù)法中，關(guān)鍵術(shù)語包括“拉格朗日乘子”、“約束條件”和“目標(biāo)函數(shù)”。目標(biāo)函數(shù)是需要優(yōu)化的函數(shù)，約束條件是變量必須滿足的限制條件，而拉格朗日乘子則是用于調(diào)整目標(biāo)函數(shù)與約束之間關(guān)系的參數(shù)。

2. 拉格朗日乘數(shù)法的數(shù)學(xué)背景

2.1 偏導(dǎo)數(shù)與梯度

在數(shù)學(xué)中，偏導(dǎo)數(shù)和梯度是求解優(yōu)化問題的基礎(chǔ)工具。偏導(dǎo)數(shù)表示函數(shù)在某一方向上的變化率，而梯度則是所有偏導(dǎo)數(shù)的向量，指向函數(shù)增長最快的方向。在拉格朗日乘數(shù)法中，梯度用于判斷目標(biāo)函數(shù)與約束條件的相切性。

2.2 極值問題與約束條件

極值問題涉及找到函數(shù)的最大值或最小值。在有約束的情況中，函數(shù)的極值點不僅要滿足目標(biāo)函數(shù)的導(dǎo)數(shù)為零，還需滿足約束條件。這時，拉格朗日乘數(shù)法通過構(gòu)造一個新的函數(shù)，結(jié)合目標(biāo)函數(shù)和約束條件，來尋找這些極值點。

3. 拉格朗日乘數(shù)法的應(yīng)用實例

3.1 實例分析：雙曲線問題

考慮麻省理工學(xué)院數(shù)學(xué)課程中的一個經(jīng)典問題：在雙曲線 $xy=3$ 上找到離原點最近的點。通過拉格朗日乘數(shù)法，我們可以將這個問題轉(zhuǎn)化為一個無約束的優(yōu)化問題，從而簡化求解過程。具體步驟包括構(gòu)建拉格朗日函數(shù)，求解偏導(dǎo)數(shù)方程組，最終得到最優(yōu)解。

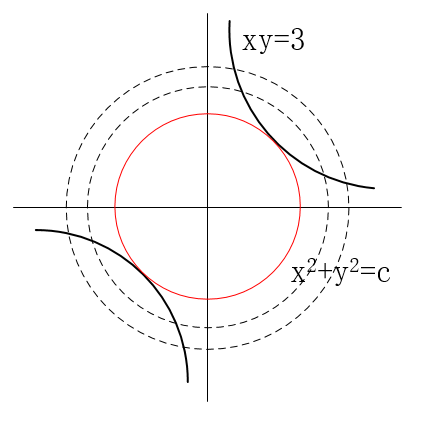
雙曲線示意圖

3.2 復(fù)雜問題中的應(yīng)用

在更復(fù)雜的優(yōu)化問題中，拉格朗日乘數(shù)法仍然表現(xiàn)出色。無論是經(jīng)濟學(xué)中的資源分配問題，還是工程學(xué)中的結(jié)構(gòu)優(yōu)化問題，拉格朗日乘數(shù)法都能通過引入多個乘子，靈活處理多約束條件的極值問題。

4. KKT條件與拉格朗日乘數(shù)法的擴展

4.1 KKT條件的定義與應(yīng)用

KKT條件，即Karush-Kuhn-Tucker條件，是拉格朗日乘數(shù)法的擴展，用于處理包含不等式約束的優(yōu)化問題。KKT條件是非線性規(guī)劃問題最優(yōu)解的必要條件，它在現(xiàn)代優(yōu)化理論中占據(jù)核心地位。

4.2 KKT條件下的優(yōu)化問題

在KKT條件下，優(yōu)化問題的解決不僅包括傳統(tǒng)的等式約束，還涉及不等式約束的處理。KKT條件通過引入對偶變量，將不等式約束轉(zhuǎn)化為等式約束，進而求解優(yōu)化問題。

5. 從線性規(guī)劃到凸優(yōu)化

5.1 線性規(guī)劃的基本步驟

線性規(guī)劃是優(yōu)化問題的一種特殊形式，通常通過消元法和單純形法求解。在此過程中，拉格朗日乘數(shù)法則提供了一種理論支持，用于解釋約束條件和最優(yōu)解之間的關(guān)系。

5.2 凸優(yōu)化中的拉格朗日方法

在凸優(yōu)化問題中，拉格朗日乘數(shù)法同樣適用。凸優(yōu)化的特點是局部最優(yōu)即為全局最優(yōu)，這使得拉格朗日乘數(shù)法在求解過程中更加高效。通過將目標(biāo)函數(shù)和約束條件構(gòu)造成凸函數(shù)，優(yōu)化問題得以簡化。

6. 實際應(yīng)用中的挑戰(zhàn)與解決方案

6.1 實際應(yīng)用中的常見問題

在實際應(yīng)用中，拉格朗日乘數(shù)法可能面臨約束條件復(fù)雜、解不唯一等問題。為了應(yīng)對這些挑戰(zhàn)，通常需要結(jié)合數(shù)值模擬和計算機輔助設(shè)計等方法，以提高解的精度和效率。

6.2 解決復(fù)雜約束的策略

為了解決復(fù)雜約束問題，可以采用迭代優(yōu)化、逐步放松約束條件等策略。同時，利用現(xiàn)代計算機技術(shù)，可以快速處理大規(guī)模數(shù)據(jù)，進一步提升拉格朗日乘數(shù)法的應(yīng)用效果。

7. 拉格朗日乘數(shù)法的未來發(fā)展方向

7.1 新領(lǐng)域的應(yīng)用

隨著科學(xué)技術(shù)的進步，拉格朗日乘數(shù)法在新興領(lǐng)域的應(yīng)用前景廣闊。例如，在機器學(xué)習(xí)中的參數(shù)優(yōu)化、圖像處理中的邊緣檢測等方面，拉格朗日乘數(shù)法都有可能發(fā)揮重要作用。

7.2 發(fā)展趨勢與前景

未來，隨著算法的不斷改進和計算能力的提升，拉格朗日乘數(shù)法將在更廣泛的領(lǐng)域內(nèi)得到應(yīng)用。尤其是在處理高維數(shù)據(jù)和多目標(biāo)優(yōu)化問題時，該方法的優(yōu)勢將更加凸顯。

FAQ

問：拉格朗日乘數(shù)法主要解決什么類型的問題？
- 答：拉格朗日乘數(shù)法主要用于解決多變量函數(shù)的極值問題，特別是在存在約束條件的情況下，如等式和不等式約束。
問：如何判斷一個問題是否適合使用拉格朗日乘數(shù)法？
- 答：如果問題涉及求解在特定約束下的最優(yōu)值，并且約束條件可以轉(zhuǎn)換為等式或不等式形式，那么拉格朗日乘數(shù)法可能是一個合適的選擇。
問：拉格朗日乘數(shù)法與KKT條件有什么關(guān)系？
- 答：KKT條件是拉格朗日乘數(shù)法的擴展，適用于包含不等式約束的優(yōu)化問題。KKT條件為求解此類問題提供了必要條件，且在凸優(yōu)化中為充要條件。