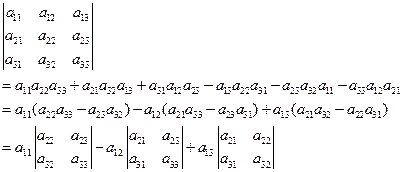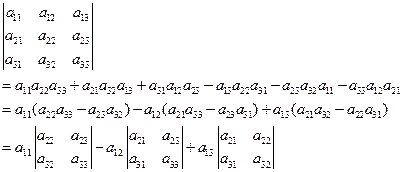1 & 1 & 1
2 & 3 & 4
end{vmatrix}$$
其余子式 $M_{32}$ 就是去掉第三行和第二列后得到的行列式:
$$M_{32} = begin{vmatrix} 1 & 0
1 & 1
end{vmatrix}$$
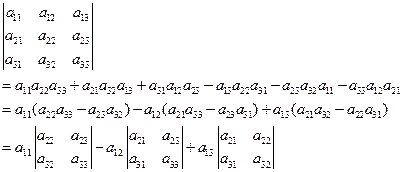
1.2 代數余子式
代數余子式是在余子式前加上 $(-1)^{i+j}$ 的符號,其中 $i$ 和 $j$ 分別表示元素的行號和列號。這樣處理是為了保持行列式展開的符號一致性。
1.3 按行(列)展開定理
行列式的值等于其任意一行(列)各元素與其代數余子式乘積之和。按行展開公式為:
$$D = a{i1}A{i1} + a{i2}A{i2} + … + a{in}A{in}$$
按列展開公式類似,適用于列的元素。選擇包含較多零元素的行(列)進行展開可以簡化計算。
2. 異乘變零定理
異乘變零定理指出,若行列式中某行(列)元素與另一行(列)元素的代數余子式相乘后累加,其和為零。這一性質在簡化計算中非常有用。
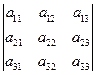
2.1 理論解釋
假設行列式 $D$:
$$D = begin{vmatrix} 1 & 1 & 2 & 3
0 & 0 & 8 & 9
2 & 2 & 5 & 4
9 & 9 & 9 & 10
end{vmatrix}$$
用第4行元素與第1行元素的代數余子式相乘:
$$9A{11} + 9A{12} + 9A{13} + 10A{14} = 0$$
2.2 應用
通過構造新的行列式驗證異乘變零定理,可以幫助我們尋找行列式的解或簡化復雜的運算過程。
3. 拉普拉斯定理
拉普拉斯定理允許我們將行列式展開為多個小階的行列式,是理解高階行列式計算的關鍵工具。
3.1 k階子式
k階子式是指從n階行列式中取定k行和k列,所形成的交叉元素構成的行列式。通過去掉這些行和列,我們得到余子式。
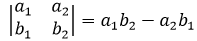
3.2 拉普拉斯展開
在n階行列式中,任意選定k行,由這些行元素組成的k階子式與對應的代數余子式乘積之和等于行列式的值。
4. 行列式相乘定理
當兩個同階行列式相乘時,其結果為一個新的行列式。行列式相乘定理為我們提供了一個計算復雜矩陣乘積的新方法。
4.1 運算規則
假設行列式 $D_1$ 和 $D_2$,相乘后的第1行第1個元素為 $D_1$ 的第1行與 $D_2$ 的第1列元素相乘之和,以此類推。
4.2 示例
$$begin{vmatrix} 1 & 1 & 1
2 & 0 & 0
0 & 0 & 3
end{vmatrix} times begin{vmatrix} 1 & 2 & 3
1 & 3 & 2
3 & 2 & 1
end{vmatrix} = begin{vmatrix} 5 & 7 & 6
2 & 4 & 6
9 & 6 & 3
end{vmatrix}$$
5. 行列式的性質
行列式的性質幫助我們理解其幾何意義和代數特性。
5.1 性質0:單位矩陣的行列式為1
單位矩陣是行列式為1的特殊矩陣。
5.2 性質1:全零行導致行列式為0
如果行列式中某行或某列元素全為0,則行列式的值為0。
5.3 性質2:成比例行導致行列式為0
如果兩行(列)成比例,則行列式為0。
6. 行列式的意義
行列式不僅是一個數值,更是向量間關系的刻畫。行列式不為零說明向量獨立,反之則不獨立。
6.1 幾何意義
行列式在幾何上表示向量圍成圖形的面積或體積。例如,二維平面中由兩個向量圍成的平行四邊形的面積就是行列式的值。
6.2 方程組解的判別
行列式的值影響方程組的解。當行列式不為零時,方程組有唯一解;為零時,可能無解或有無數解。
7. 行列式計算技巧
利用行列式的性質和定理,我們可以簡化計算。
7.1 消元法
通過消元法將矩陣轉換為上三角矩陣,行列式的值等于主對角線元素的乘積。
7.2 行列式公式
行列式的公式可以用于計算復雜矩陣的行列式值。對于n階矩陣,行列式的計算復雜度通常較高,但公式提供了一種系統化的計算方法。
FAQ
-
問:行列式展開的實用意義是什么?
- 答:行列式展開使得高階行列式的計算變得可行,并且是線性代數中許多其他定理和應用的基礎。
-
問:如何選擇展開的行或列?
- 答:通常選擇包含最多零元素的行或列進行展開,以簡化計算過程。
-
問:行列式值為零意味著什么?
- 答:行列式值為零意味著矩陣行或列之間存在線性相關性,導致解的獨立性喪失。
-
問:行列式如何應用于方程組求解?
- 答:通過行列式可以判斷方程組的解是否唯一,并通過克拉默法則求解。
-
問:行列式的幾何解釋是什么?
- 答:行列式在幾何上表示由向量圍成圖形的面積或體積,反映了向量的獨立性。
熱門推薦
一個賬號試用1000+ API
助力AI無縫鏈接物理世界 · 無需多次注冊
3000+提示詞助力AI大模型
和專業工程師共享工作效率翻倍的秘密
国内精品久久久久影院日本,日本中文字幕视频,99久久精品99999久久,又粗又大又黄又硬又爽毛片
欧美日韩免费电影|
91麻豆免费在线观看|
国产精品色婷婷久久58|
久久精品免费观看|
久久品道一品道久久精品|
国产在线看一区|
欧美激情一区不卡|
欧洲一区在线观看|
一区二区不卡在线视频 午夜欧美不卡在
|
欧美日韩免费观看一区二区三区|
亚洲一区二区五区|
欧美成人一区二区三区片免费|
极品少妇xxxx偷拍精品少妇|
欧美激情一区二区在线|
91麻豆产精品久久久久久|
无吗不卡中文字幕|
国产精品色婷婷久久58|
日韩一区二区三区电影在线观看|
国产综合成人久久大片91|
亚洲三级在线看|
日韩精品一区二区三区在线观看
|
婷婷亚洲久悠悠色悠在线播放|
精品sm捆绑视频|
色哟哟一区二区在线观看|
免费美女久久99|
18涩涩午夜精品.www|
日韩一区二区免费电影|
色拍拍在线精品视频8848|
黄色小说综合网站|
亚洲丰满少妇videoshd|
国产精品久久久久婷婷二区次|
欧美成人艳星乳罩|
91精品国产欧美一区二区成人
|
亚洲乱码中文字幕|
中文欧美字幕免费|
久久久高清一区二区三区|
91精品蜜臀在线一区尤物|
91蜜桃在线观看|
av色综合久久天堂av综合|
国精产品一区一区三区mba桃花|
樱花草国产18久久久久|
亚洲另类在线制服丝袜|
亚洲三级在线看|
...av二区三区久久精品|
国产精品网站在线|
国产精品福利影院|
国产色产综合产在线视频|
精品少妇一区二区三区在线视频|
欧美日韩在线免费视频|
欧美午夜一区二区三区免费大片|
一本色道久久综合亚洲精品按摩|
色综合中文字幕国产|
国产一区二区三区黄视频|
久久99国产精品久久99|
精品亚洲免费视频|
成人一区二区三区|
91色婷婷久久久久合中文|
色拍拍在线精品视频8848|
日本道免费精品一区二区三区|
在线视频一区二区免费|
欧美精品第1页|
欧美精品一区二区三区视频|
久久久久久日产精品|
中文字幕第一区综合|
亚洲卡通欧美制服中文|
亚洲福利视频一区二区|
国内精品久久久久影院薰衣草|
国产高清不卡一区二区|
日本韩国欧美一区|
精品av综合导航|
一区二区三区不卡视频|
久草这里只有精品视频|
99久久国产综合精品麻豆|
91麻豆精品国产|
亚洲三级在线免费|
国产综合久久久久影院|
欧美手机在线视频|
日本一区二区三区高清不卡|
亚洲一本大道在线|
成人久久18免费网站麻豆|
在线播放视频一区|
亚洲男人都懂的|
国产成人综合网|
337p亚洲精品色噜噜|
亚洲天堂2016|
成人一区二区在线观看|
精品国产网站在线观看|
天堂av在线一区|
91精品福利视频|
欧美国产精品劲爆|
国产一区二区三区高清播放|
欧美日韩一区小说|
亚洲综合色自拍一区|
波多野结衣精品在线|
国产日本亚洲高清|
极品美女销魂一区二区三区免费|
欧美三级视频在线观看|
亚洲乱码一区二区三区在线观看|
丁香另类激情小说|
中文乱码免费一区二区|
国产成人亚洲综合色影视|
久久久亚洲精华液精华液精华液
|
天天操天天色综合|
欧美疯狂做受xxxx富婆|
亚洲一区成人在线|
欧美视频一区二区在线观看|
亚洲精品一卡二卡|
色呦呦国产精品|
亚洲乱码一区二区三区在线观看|
波多野结衣亚洲|
国产精品久久久久天堂|
91年精品国产|
亚洲一区二区三区影院|
欧美午夜精品一区二区蜜桃|
亚洲五月六月丁香激情|
欧美电影影音先锋|
国产自产v一区二区三区c|
国产欧美日韩另类一区|
成人亚洲一区二区一|
亚洲日本免费电影|
在线中文字幕一区|
日韩电影免费在线|
www日韩大片|
成人丝袜视频网|
亚洲精品一二三|
欧美一卡2卡3卡4卡|
久久成人免费网站|
亚洲裸体xxx|
久久综合久色欧美综合狠狠|
风间由美一区二区三区在线观看|
亚洲人xxxx|
久久午夜老司机|
欧美午夜宅男影院|
成人美女视频在线观看|
日韩二区在线观看|
欧美韩国日本一区|
欧美一区二区三区喷汁尤物|
av资源网一区|
国产在线精品一区二区|
亚洲国产精品欧美一二99|
精品国产露脸精彩对白|
91在线国内视频|
精品中文字幕一区二区|
亚洲精品视频在线看|
www成人在线观看|
欧美日韩视频第一区|
91香蕉视频mp4|
国产精品1区2区3区在线观看|
午夜在线电影亚洲一区|
亚洲素人一区二区|
久久久美女毛片|
欧美大片在线观看一区二区|
欧美伊人久久久久久久久影院
|
国产在线精品一区二区夜色|
亚洲成人午夜电影|
亚洲男人天堂一区|
亚洲欧美在线观看|
欧美国产一区二区在线观看|
精品粉嫩超白一线天av|
精品日韩成人av|
日韩欧美国产综合在线一区二区三区|
欧美系列日韩一区|
欧美日韩国产经典色站一区二区三区|
91久久国产综合久久|
91视视频在线直接观看在线看网页在线看|
久久99精品国产麻豆婷婷|
爽好多水快深点欧美视频|
亚洲成人精品一区二区|
偷拍日韩校园综合在线|
日韩电影在线观看电影|
蜜臀va亚洲va欧美va天堂
|
欧美bbbbb|
久久精品国产一区二区三
|
91精品国产综合久久精品图片|
色琪琪一区二区三区亚洲区|
色婷婷综合久久久|
欧美怡红院视频|
日韩色视频在线观看|
亚洲精品在线观|
国产精品人人做人人爽人人添|
国产精品五月天|
亚洲国产你懂的|
日韩中文字幕亚洲一区二区va在线|
午夜天堂影视香蕉久久|
蜜臀av性久久久久蜜臀aⅴ四虎|
久久精品国产77777蜜臀|
粉嫩久久99精品久久久久久夜|
色综合中文综合网|
久久婷婷久久一区二区三区|
中文在线一区二区|
亚洲国产欧美日韩另类综合
|
欧美唯美清纯偷拍|
久久奇米777|
亚洲国产裸拍裸体视频在线观看乱了
|
日韩视频免费观看高清在线视频|
欧美高清在线一区|
久久精品国产999大香线蕉|
在线视频国产一区|
国产欧美日韩视频在线观看|
婷婷开心激情综合|