
實(shí)時(shí)航班追蹤背后的技術(shù):在線飛機(jī)追蹤器的工作原理
一次函數(shù),或稱線性函數(shù),具有形式 $y = mx + b$。其圖像是一條直線,其中 $m$ 是斜率,決定了直線的傾斜程度,而 $b$ 是截距,表示直線在 $y$ 軸上的交點(diǎn)。一次函數(shù)廣泛用于描述線性關(guān)系。

反比例函數(shù)的形式為 $y = frac{1}{x}$。其圖像是一條雙曲線,分布在第一和第三象限,隨著 $x$ 的絕對(duì)值增大,函數(shù)值逐漸接近于零。反比例函數(shù)常用于描述反向相關(guān)的關(guān)系。

二次函數(shù)以 $y = ax^2 + bx + c$ 表示,其圖像是一條拋物線。參數(shù) $a$ 決定了拋物線的開口方向和寬窄,$b$ 和 $c$ 影響其頂點(diǎn)的位置。二次函數(shù)在物理學(xué)中用于描述拋物運(yùn)動(dòng)。

指數(shù)函數(shù)具有形式 $y = a^x$,其中 $a$ 是底數(shù)。其圖像隨 $x$ 增大呈指數(shù)增長(zhǎng),當(dāng) $0 < a < 1$ 時(shí),函數(shù)是遞減的。當(dāng) $a > 1$ 時(shí),函數(shù)是遞增的。指數(shù)函數(shù)廣泛應(yīng)用于金融和人口增長(zhǎng)模型中。

正弦函數(shù) $ ext{sin}(x)$ 是周期函數(shù),其圖像是一條波動(dòng)的曲線,周期為 $2pi$。正弦函數(shù)常用于描述周期性現(xiàn)象,如聲波和光波。

余弦函數(shù) $ ext{cos}(x)$ 也是周期函數(shù),與正弦函數(shù)相似,但其相位不同,周期同樣為 $2pi$。余弦函數(shù)用于描述振動(dòng)和波動(dòng)現(xiàn)象。

正切函數(shù) $ ext{tan}(x)$ 的周期為 $pi$,其圖像在每個(gè)周期內(nèi)有不連續(xù)的豎直漸近線。正切函數(shù)用于表示角度的比率。

反正弦函數(shù) $ ext{arcsin}(x)$ 是正弦函數(shù)的反函數(shù),其定義域?yàn)?$[-1, 1]$,值域?yàn)?$[-frac{pi}{2}, frac{pi}{2}]$。反正弦函數(shù)用于計(jì)算給定正弦值對(duì)應(yīng)的角度。

反余弦函數(shù) $ ext{arccos}(x)$ 對(duì)應(yīng)余弦函數(shù),其定義域?yàn)?$[-1, 1]$,值域?yàn)?$[0, pi]$。反余弦函數(shù)用于計(jì)算給定余弦值對(duì)應(yīng)的角度。

反正切函數(shù) $ ext{arctan}(x)$ 是正切函數(shù)的反函數(shù),其圖像在 $(-infty, infty)$ 上連續(xù)。反正切函數(shù)用于計(jì)算給定正切值對(duì)應(yīng)的角度。

三角函數(shù)的兩角和與差公式幫助我們將多個(gè)角度的函數(shù)簡(jiǎn)化為更易處理的形式。例如:
這些公式廣泛應(yīng)用于物理和工程計(jì)算中,尤其是在波動(dòng)和信號(hào)處理領(lǐng)域。

倍角公式用于將角度的倍數(shù)函數(shù)表示為單個(gè)角度的函數(shù),如:
倍角公式在多角度問題中非常有用,如計(jì)算光的干涉和衍射。
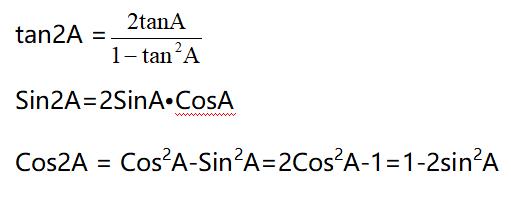
半角公式用于將半角的三角函數(shù)表示為單角的函數(shù):
這些公式在計(jì)算精度要求高的場(chǎng)合非常重要,如數(shù)值分析。
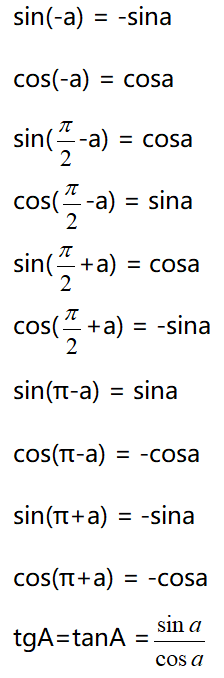
問:函數(shù)圖像如何幫助我們理解函數(shù)的性質(zhì)?
問:如何使用三角函數(shù)公式解決實(shí)際問題?
問:反三角函數(shù)在計(jì)算中有哪些應(yīng)用?
通過本文的詳細(xì)講解,我們希望您能更好地理解函數(shù)圖像及其相關(guān)的三角函數(shù)公式,并能夠應(yīng)用于實(shí)際問題的解決中。
對(duì)比大模型API的內(nèi)容創(chuàng)意新穎性、情感共鳴力、商業(yè)轉(zhuǎn)化潛力
一鍵對(duì)比試用API 限時(shí)免費(fèi)