亚洲视频在线播放,桃色国产精品站一桃色阁,久草视频资源在线

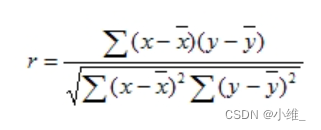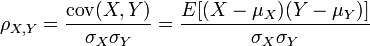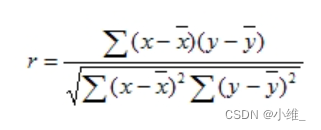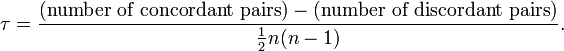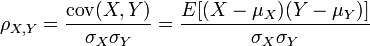
公式中，cov(X, Y)是X和Y的協(xié)方差，σX是X的標(biāo)準(zhǔn)差，μX是X的期望。

代碼示例：

a <- c(1, 2, 3)
b <- c(11, 12, 14)
cor.test(a, b, method="pearson")

圖示：為了形象化地理解皮爾遜相關(guān)系數(shù)，我們通常會(huì)使用散點(diǎn)圖來展示數(shù)據(jù)點(diǎn)的分布。
Pearson相關(guān)系數(shù)圖示

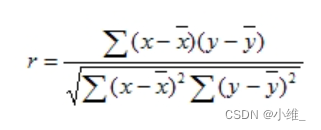
3：斯皮爾曼相關(guān)系數(shù)（Spearman Rank Correlation Coefficient）

斯皮爾曼相關(guān)系數(shù)是一種非參數(shù)的相關(guān)性分析方法，適用于對(duì)數(shù)據(jù)的等級(jí)順序進(jìn)行分析。與皮爾遜相關(guān)系數(shù)不同，斯皮爾曼相關(guān)系數(shù)不需要數(shù)據(jù)呈正態(tài)分布，因而更適合于處理偏態(tài)數(shù)據(jù)或有序數(shù)據(jù)。

公式說明：斯皮爾曼相關(guān)系數(shù)的計(jì)算方式類似于皮爾遜相關(guān)系數(shù)，只需要將原始數(shù)據(jù)替換為排名數(shù)據(jù)。

代碼示例：

a <- c(1, 10, 100, 101)
b <- c(21, 10, 15, 13)
cor.test(a, b, method="spearman")

應(yīng)用場景：斯皮爾曼相關(guān)系數(shù)廣泛應(yīng)用于非線性關(guān)系的檢測，如在教育領(lǐng)域分析學(xué)生成績排名之間的相關(guān)性。

4：肯德爾相關(guān)系數(shù)（Kendall’s Tau Correlation Coefficient）

肯德爾相關(guān)系數(shù)用于衡量兩個(gè)變量之間的排序一致性。它通過計(jì)算和諧對(duì)與不和諧對(duì)的數(shù)量差，來判斷變量之間的相關(guān)性。

公式說明：

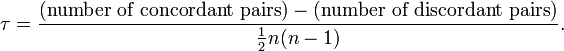
代碼示例：

a <- c(1, 2, 3)
b <- c(1, 3, 2)
cor.test(a, b, method="kendall")

應(yīng)用場景：適用于小樣本數(shù)據(jù)和存在重復(fù)值的情況，常用于社會(huì)科學(xué)研究中。

5：多變量相關(guān)性分析

多變量相關(guān)性分析用于研究多個(gè)變量之間的關(guān)系。主成分分析（PCA）和因子分析是其中的常見方法，主要用于降維和識(shí)別主要相關(guān)性模式。

PCA示例：通過PCA可以將高維數(shù)據(jù)降維，保留主要信息，有助于數(shù)據(jù)可視化和模型構(gòu)建。

6：相關(guān)性分析在數(shù)據(jù)科學(xué)中的應(yīng)用

在數(shù)據(jù)科學(xué)中，相關(guān)性分析是數(shù)據(jù)清洗和特征選擇的重要工具。它幫助數(shù)據(jù)科學(xué)家識(shí)別重要變量、消除多重共線性，提高模型的預(yù)測能力。

7：結(jié)論與未來展望

相關(guān)性分析為我們提供了一個(gè)強(qiáng)大的工具，可以幫助理解復(fù)雜數(shù)據(jù)集中的變量關(guān)系。隨著數(shù)據(jù)量和復(fù)雜性的增加，相關(guān)性分析將在大數(shù)據(jù)分析、機(jī)器學(xué)習(xí)和人工智能領(lǐng)域發(fā)揮更重要的作用。通過不斷發(fā)展和深化這些分析方法，我們將能夠從數(shù)據(jù)中獲取更豐富的洞察。

FAQ

問：相關(guān)系數(shù)的取值范圍是什么？
- 答：相關(guān)系數(shù)的取值范圍是-1到1。其中，1表示完全正相關(guān)，-1表示完全負(fù)相關(guān)，0表示無相關(guān)性。
問：如何選擇合適的相關(guān)系數(shù)分析方法？
- 答：選擇相關(guān)系數(shù)分析方法主要取決于數(shù)據(jù)的類型和分布。皮爾遜相關(guān)系數(shù)適用于正態(tài)分布的連續(xù)數(shù)據(jù)，斯皮爾曼和肯德爾相關(guān)系數(shù)適用于非正態(tài)分布或有序數(shù)據(jù)。
問：相關(guān)性分析與因果關(guān)系有何不同？
- 答：相關(guān)性分析僅揭示變量之間的關(guān)系強(qiáng)度和方向，并不表示因果關(guān)系。因果關(guān)系需要通過實(shí)驗(yàn)設(shè)計(jì)和因果推斷來驗(yàn)證。