季節性

季節性指的是在固定時間間隔內重復出現的模式。識別季節性有助于預測周期性的變化，例如每年的氣溫波動。

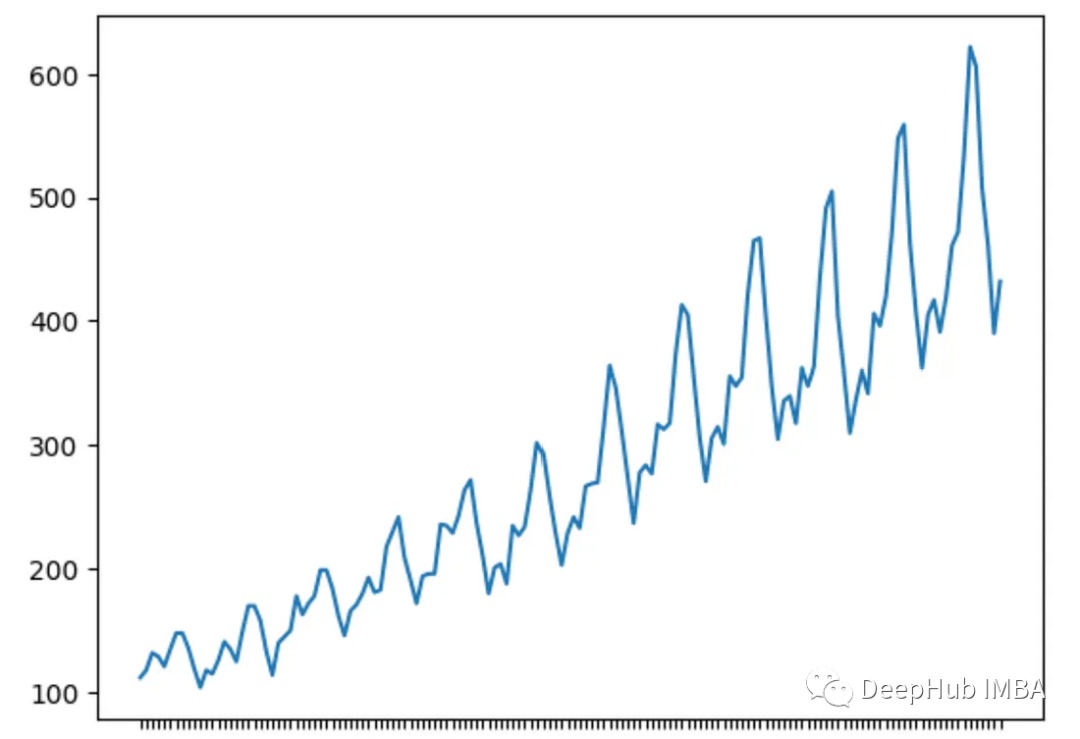
殘差或白噪聲

殘差是時間序列中無法用趨勢或季節性解釋的隨機性，通常被視為白噪聲。理解殘差有助于評估模型的預測誤差。

時間序列分解與預測

時間序列分解

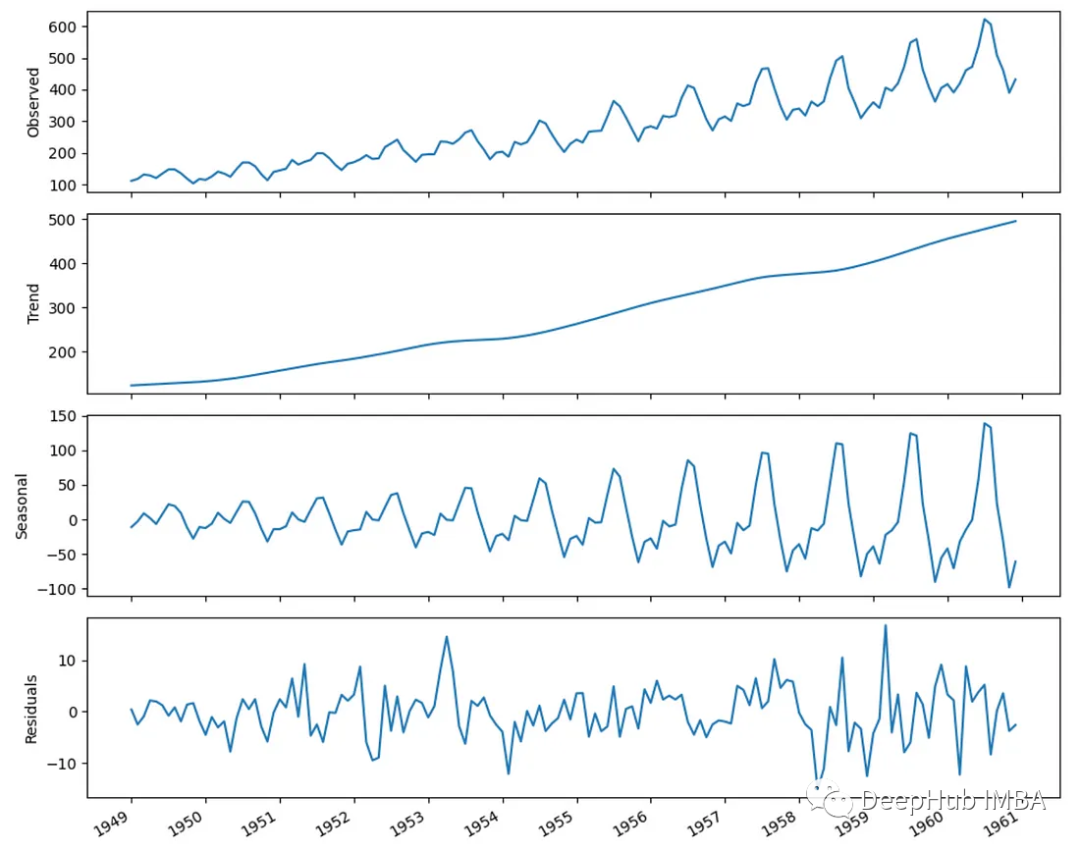
時間序列分解是將序列分解為趨勢、季節性和殘差的過程。可以使用統計工具如 statsmodels 庫中的 STL 函數來實現。

import pandas as pd 
import matplotlib.pyplot as plt
from statsmodels.tsa.seasonal import STL

df = pd.read_csv('time-series-data.csv')
decomposition = STL(df['x'], period=12).fit()

分解后的時間序列可以幫助我們更好地理解數據中每個組成部分的影響。

時間序列預測

預測是一種利用歷史數據來推測未來數據點的技術，經常使用的模型包括自回歸模型（AR）、移動平均模型（MA）、自回歸移動平均模型（ARMA）等。對于復雜的數據集，深度學習模型如長短期記憶網絡（LSTM）也可以用于時間序列預測。

預測模型的基本步驟

1. 收集數據：收集時間序列數據，并確保數據質量。
2. 開發預測模型：基于歷史數據，選擇合適的模型進行訓練。
3. 部署模型：將訓練好的模型應用于實際場景。
4. 模型評估與調整：監控模型性能，進行必要的調整和重新訓練。

平穩性與變換

平穩性

平穩性是時間序列的一個重要屬性，指序列的統計特征（如均值和方差）不隨時間變化。平穩序列對于許多統計預測模型來說是理想的，因為這些模型通常假設數據是平穩的。

變換

為了獲得平穩序列，常用的方法包括差分、對數變換等。這些方法可以幫助減小數據中的波動，使其更適合模型構建。

自相關與偏自相關

自相關

自相關是指時間序列中不同時間點之間的線性關系，通常通過自相關函數（ACF）圖來分析。

from statsmodels.graphics.tsaplots import plot_acf

plot_acf(time_series, lags=20)

偏自相關

偏自相關是指消除較短滯后影響后，某一滯后期的自相關程度。偏自相關函數（PACF）圖可以幫助確定模型中自回歸項的個數。

平滑方法

平滑方法用于減少數據中的隨機噪聲，以便更好地觀察趨勢和季節性。常見的方法有移動平均法、指數平滑法等。

時間序列數據特征

靜態時間序列

靜態時間序列假設數據在時間上的特征不變，常用于平均數模型和指數平滑模型。

動態時間序列

動態時間序列考慮數據隨時間的變化，常用于ARIMA和VAR等模型。

FAQ

1. 問：什么是時間序列分析的主要步驟？

   • 答：時間序列分析主要包括數據收集、數據預處理、特征分析、模型選擇、模型訓練和模型評估。

2. 問：如何判斷一個時間序列是否平穩？

   • 答：可以通過繪制序列圖、計算ADF檢驗等方法來判斷時間序列的平穩性。

3. 問：什么是自相關圖？

   • 答：自相關圖是一種用于顯示時間序列中不同時間點間相關性的工具，幫助識別序列中的模式和規律。

時間序列分析是一個復雜而重要的領域，掌握其基本概念和技術不僅有助于學術研究，也能在商業應用中發揮重大作用。