
openai.chatcompletion.create用法和圖片鏈接詳解
算法應具備五大特征:有窮性、確切性、輸入項、輸出項和可行性。
這些特征確保算法是能夠在現實中被有效執行的。
計算機的基本操作分為四類:
算法的功能不僅依賴于操作本身,還與操作的執行順序密切相關。良好的控制結構可以提高算法的效率。
算法的質量通常通過以下標準來評估:

冒泡排序通過重復地遍歷待排序列,比較相鄰元素并交換錯誤順序的元素來進行排序。它的時間復雜度為O(n^2),在輸入數據已經有序時效率最高。
def bubbleSort(nums):
for i in range(len(nums) - 1):
for j in range(len(nums) - i - 1):
if nums[j] > nums[j+1]:
nums[j], nums[j+1] = nums[j+1], nums[j]
return nums
選擇排序在每次遍歷中選擇最小的元素,放到已排序的序列末尾。其時間復雜度為O(n^2),不受輸入數據影響。
def selectionSort(nums):
for i in range(len(nums) - 1):
minIndex = i
for j in range(i + 1, len(nums)):
if nums[j] < nums[minIndex]:
minIndex = j
nums[i], nums[minIndex] = nums[minIndex], nums[i]
return nums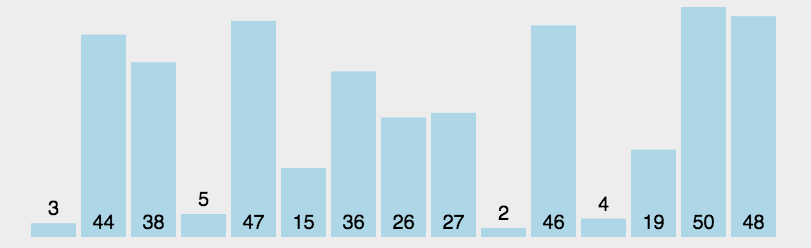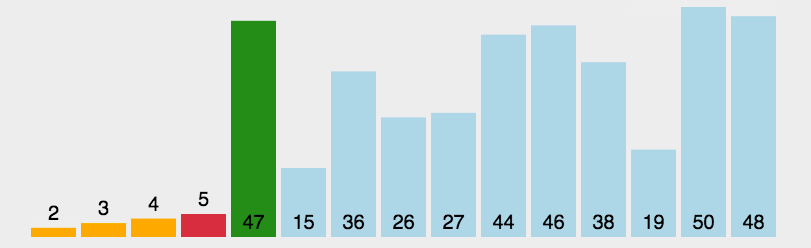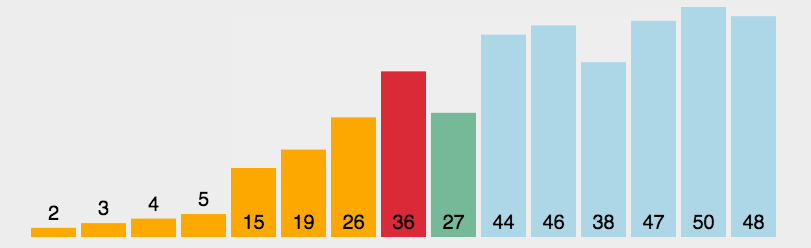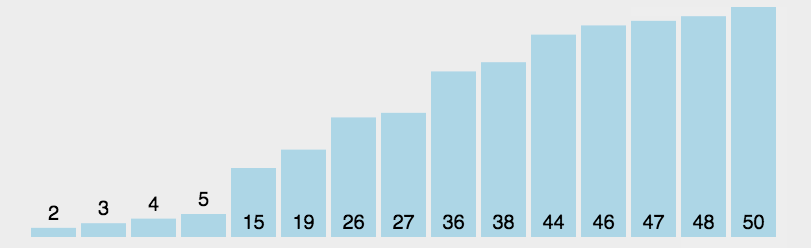
插入排序模擬整理撲克牌的手法,每次將新元素插入到已排序的部分中。雖然平均時間復雜度為O(n^2),但在部分有序序列中表現良好。
def insertionSort(nums):
for i in range(len(nums) - 1):
curNum, preIndex = nums[i+1], i
while preIndex >= 0 and curNum < nums[preIndex]:
nums[preIndex + 1] = nums[preIndex]
preIndex -= 1
nums[preIndex + 1] = curNum
return nums
希爾排序是插入排序的優化版本,通過比較距離較遠的元素來加快排序速度。它的時間復雜度為O(n log n)。
def shellSort(nums):
lens = len(nums)
gap = 1
while gap 0:
for i in range(gap, lens):
curNum, preIndex = nums[i], i - gap
while preIndex >= 0 and curNum < nums[preIndex]:
nums[preIndex + gap] = nums[preIndex]
preIndex -= gap
nums[preIndex + gap] = curNum
gap //= 3
return nums
歸并排序采用分治法,將序列遞歸拆分直至每部分僅含一個元素,然后合并排序。其時間復雜度為O(n log n),但需要額外內存。
def mergeSort(nums):
def merge(left, right):
result = []
i = j = 0
while i < len(left) and j < len(right):
if left[i] <= right[j]:
result.append(left[i])
i += 1
else:
result.append(right[j])
j += 1
result += left[i:] + right[j:]
return result
if len(nums) <= 1:
return nums
mid = len(nums) // 2
left = mergeSort(nums[:mid])
right = mergeSort(nums[mid:])
return merge(left, right)
快速排序是基于分治法的高效排序算法,常用于大數據集。其時間復雜度平均為O(n log n),盡管最壞情況下為O(n2)。
def quickSort(nums):
if len(nums) <= 1:
return nums
pivot = nums[0]
left = [x for x in nums[1:] if x = pivot]
return quickSort(left) + [pivot] + quickSort(right)
堆排序將序列構建為大根堆或小根堆,通過調整堆結構進行排序。其時間復雜度為O(n log n)。
def heapSort(nums):
def adjustHeap(nums, i, size):
lchild = 2 * i + 1
rchild = 2 * i + 2
largest = i
if lchild nums[largest]:
largest = lchild
if rchild nums[largest]:
largest = rchild
if largest != i:
nums[largest], nums[i] = nums[i], nums[largest]
adjustHeap(nums, largest, size)
def builtHeap(nums, size):
for i in range(len(nums)//2)[::-1]:
adjustHeap(nums, i, size)
size = len(nums)
builtHeap(nums, size)
for i in range(len(nums))[::-1]:
nums[0], nums[i] = nums[i], nums[0]
adjustHeap(nums, 0, i)
return nums
計數排序為線性時間復雜度的排序算法,適用于值域不大的整數序列。
def countingSort(nums):
bucket = [0] * (max(nums) + 1)
for num in nums:
bucket[num] += 1
i = 0
for j in range(len(bucket)):
while bucket[j] > 0:
nums[i] = j
bucket[j] -= 1
i += 1
return nums
桶排序是計數排序的升級版,適合均勻分布的數據。其效率取決于桶的數量和數據分布。
def bucketSort(nums, defaultBucketSize=5):
maxVal, minVal = max(nums), min(nums)
bucketSize = defaultBucketSize
bucketCount = (maxVal - minVal) // bucketSize + 1
buckets = [[] for _ in range(bucketCount)]
for num in nums:
buckets[(num - minVal) // bucketSize].append(num)
nums.clear()
for bucket in buckets:
insertionSort(bucket)
nums.extend(bucket)
return nums基數排序適用于多關鍵字排序,常用的LSD方法從低位到高位排序。
def radixSort(nums):
mod = 10
div = 1
mostBit = len(str(max(nums)))
buckets = [[] for _ in range(mod)]
while mostBit:
for num in nums:
buckets[num // div % mod].append(num)
i = 0
for bucket in buckets:
while bucket:
nums[i] = bucket.pop(0)
i += 1
div *= 10
mostBit -= 1
return nums
外部排序用于處理無法全部載入內存的大數據集,通常采用歸并排序法。其核心在于如何高效地進行子文件的劃分和歸并。
問:什么是算法的時間復雜度?
問:如何選擇合適的排序算法?
問:什么是外部排序?
問:為什么快速排序通常優于歸并排序?
問:排序算法的穩定性如何判斷?