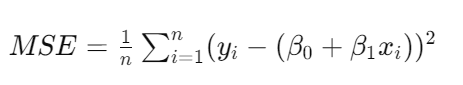
其中,( y ) 是目標變量,( x ) 是特征變量,( \beta_0 ) 和 ( \beta_1 ) 分別為截距和斜率,( \epsilon ) 是誤差項。我們通過最小化均方誤差(Mean Squared Error, MSE)來估計這些參數:
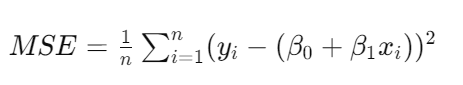
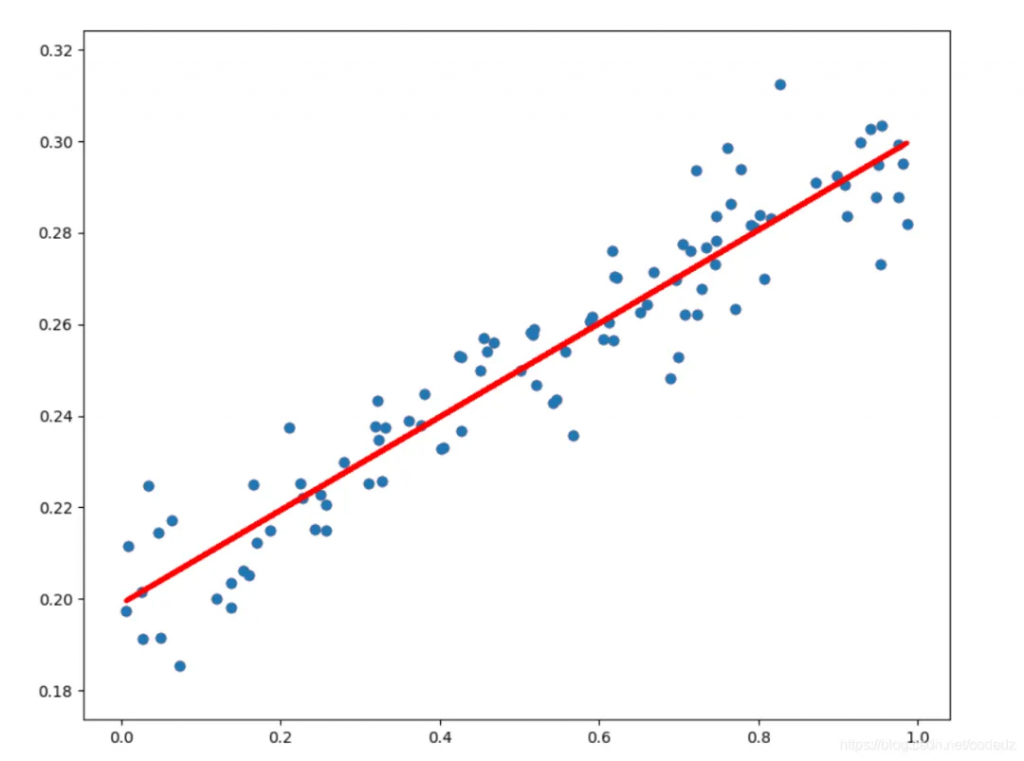
步驟:
優缺點:
優點:
缺點:
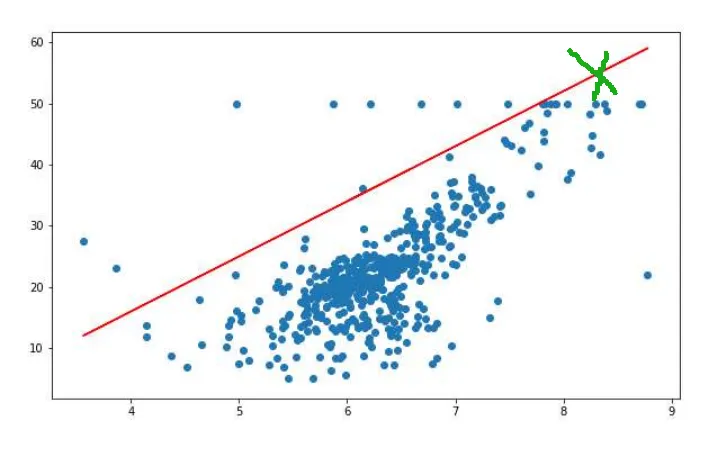
(圖:對異常值敏感)
應用場景:
線性回歸在經濟學、金融學、社會學等領域有廣泛應用。以下是一些具體的應用場景:
案例分析:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
# 設置matplotlib支持中文顯示
plt.rcParams['font.sans-serif'] = ['SimHei'] # 設置中文顯示
plt.rcParams['axes.unicode_minus'] = False # 正確顯示負號
# 創建武俠世界中的功力(X)與成名年數(y)的數據
X = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10]).reshape(-1, 1) # 功力等級
y = np.array([2, 3, 3.5, 5, 6, 7.5, 8, 9, 10.5, 11]) # 成名年數
# 使用線性回歸模型
model = LinearRegression()
model.fit(X, y) # 訓練模型
# 預測功力等級對應的成名年數
X_predict = np.array([11, 12, 13]).reshape(-1, 1) # 新的功力等級
y_predict = model.predict(X_predict) # 進行預測
# 繪制功力與成名年數的關系
plt.scatter(X, y, color='red', label='實際成名年數') # 原始數據點
plt.plot(X, model.predict(X), color='blue', label='功力成名模型') # 擬合的直線
plt.scatter(X_predict, y_predict, color='green', label='預測成名年數') # 預測點
plt.xlabel('功力等級')
plt.ylabel('成名年數')
plt.title('武俠世界的功力與成名年數關系')
plt.legend()
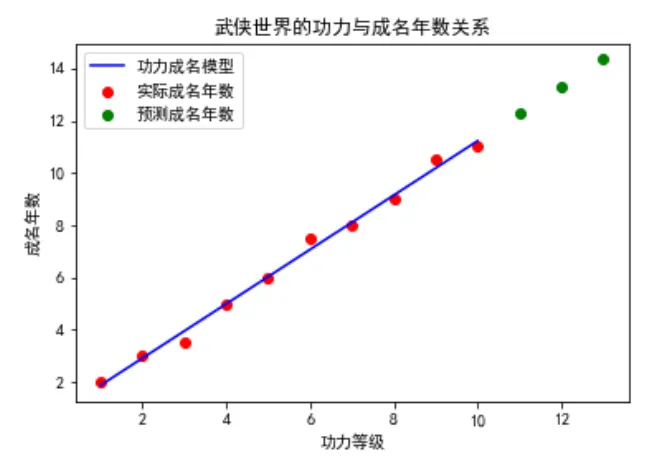
plt.show()我們首先創建了一組簡單的數據,模擬武俠世界中的人物功力等級與他們成名所需年數之間的關系。
然后,我們使用了線性回歸模型來擬合這些數據,并對新的功力等級進行了成名年數的預測。
最后,通過繪圖展示了功力等級與成名年數之間的線性關系,以及模型的預測效果。
背景:
邏輯回歸(Logistic Regression)最早由英國統計學家 David Cox 于 1958 年提出,盡管其名稱中包含“回歸”二字,但它實際上是一種分類算法,主要用于解決二分類問題。隨著計算能力的提升和數據量的增加,邏輯回歸在醫學、金融、社會科學等領域得到了廣泛應用,成為統計學習和機器學習的重要工具之一。
原理:
邏輯回歸通過一個邏輯函數(logistic function)將線性回歸的輸出映射到一個 (0, 1) 區間,從而進行二分類。其數學模型為:
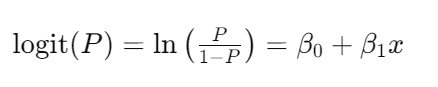
其中,( P ) 是事件發生的概率,( x ) 是特征變量,( \beta_0 ) 和 ( \beta_1 ) 分別為截距和系數。最終,通過最大似然估計法(Maximum Likelihood Estimation, MLE)來估計這些參數。
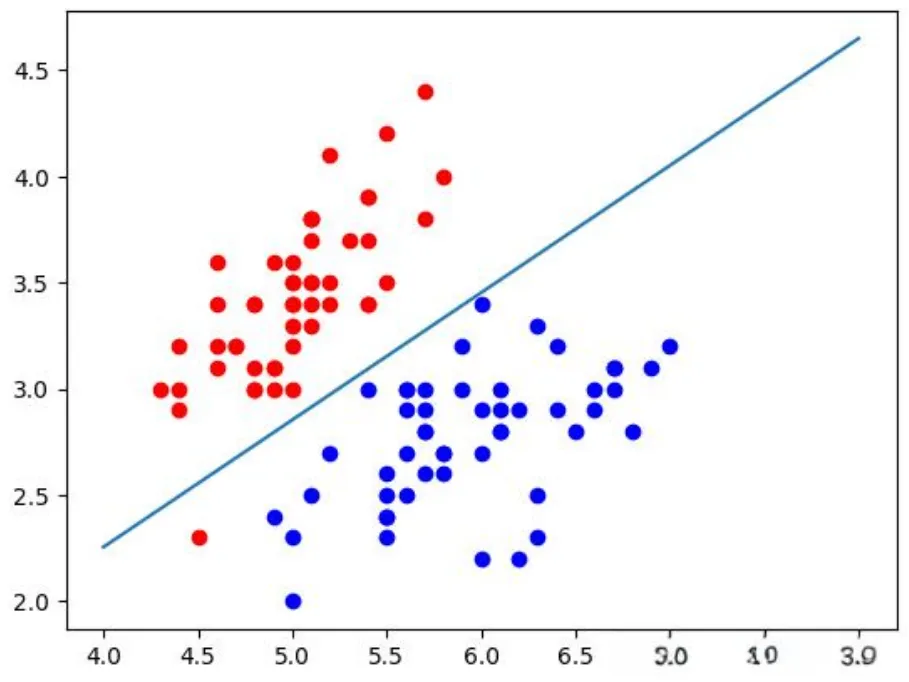
特別的,Sigmoid 函數
Sigmoid 函數:邏輯回歸中使用的Sigmoid函數 能將任意實數值映射到 (0, 1) 區間,便于解釋為概率。
一圖勝千言:
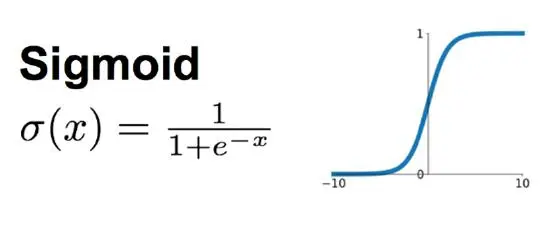
具體步驟包括:
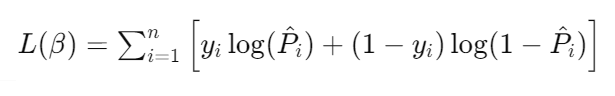
優缺點:
優點:
缺點:
應用場景:
邏輯回歸在醫學診斷、市場營銷、信用評分等領域有廣泛應用。以下是一些具體的應用場景:
案例分析:
from sklearn.linear_model import LogisticRegression
from sklearn.datasets import make_classification
import matplotlib.pyplot as plt
import numpy as np
# 生成模擬的武俠世界功力和內功心法數據集
X, y = make_classification(n_samples=100, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=42)
# 創建邏輯回歸模型對象
lr = LogisticRegression()
# 訓練模型
lr.fit(X, y)
# 定義決策邊界繪制函數
def plot_decision_boundary(X, y, model):
# 設置最小和最大值,以及增量
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.1),
np.arange(y_min, y_max, 0.1))
# 預測整個網格的值
Z = model.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
# 繪制決策邊界和散點圖
plt.contourf(xx, yy, Z, alpha=0.4)
plt.scatter(X[:, 0], X[:, 1], c=y, s=20, edgecolor='k')
plt.xlabel('功力')
plt.ylabel('內功心法')
plt.title('武俠世界中的高手分類圖')
# 繪制決策邊界和數據點
plot_decision_boundary(X, y, lr)
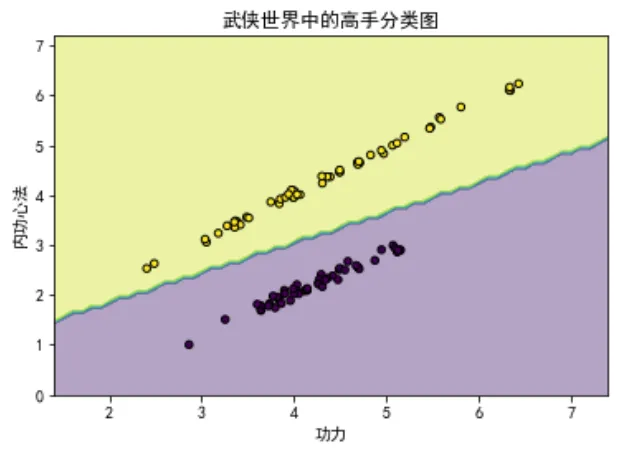
plt.show()我們首先使用make_classification函數生成了一組模擬的二維數據,模擬武俠世界中的人物根據其功力和內功心法被分為兩類:普通武者和高手。
然后,我們訓練了一個邏輯回歸模型并繪制了決策邊界,以及不同類別的樣本點,直觀展示了模型的分類效果。
在圖形中,我們可以看到如何根據功力和內功心法來區分不同的武俠人物。

背景:
梯度下降法(Gradient Descent)由法國數學家 Augustin-Louis Cauchy 在 1847 年提出,是一種用于尋找函數最小值(或最大值)的迭代優化算法。梯度下降在機器學習中尤為重要,因為它是許多算法(如線性回歸、邏輯回歸和神經網絡)中用于參數優化的核心方法。
原理:
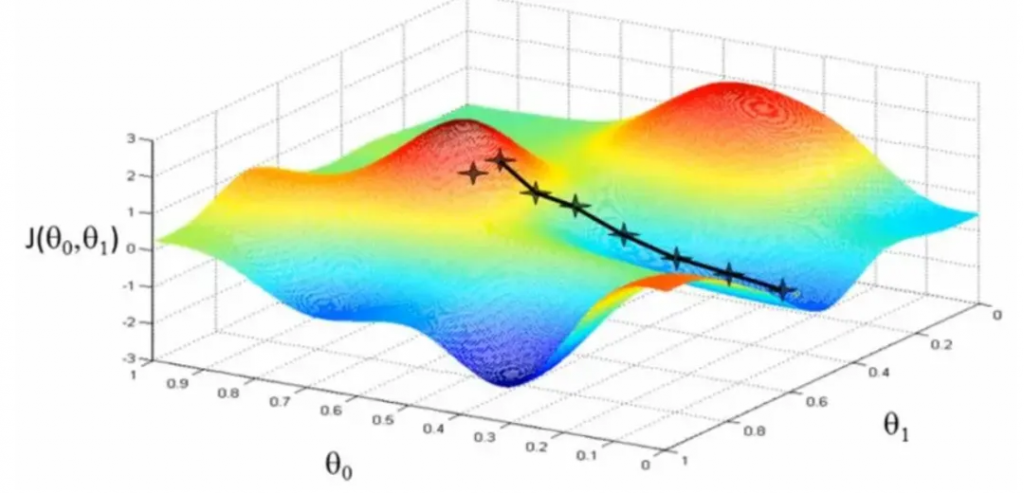
梯度下降的基本思想是從一個初始點開始,沿著函數的負梯度方向迭代更新參數,以最小化損失函數。梯度是函數在該點的偏導數向量,表示函數在該點的變化方向。梯度下降的更新公式為:

具體步驟包括:
類型:
梯度下降有幾種常見的變種:
優缺點:
優點:
缺點:
應用場景:
梯度下降廣泛應用于各種機器學習模型的訓練過程中。以下是一些具體的應用場景:
案例分析:
import numpy as np
import matplotlib.pyplot as plt
# 示例數據
X = np.array([[1, 1], [1, 2], [2, 2], [2, 3]])
y = np.dot(X, np.array([1, 2])) + 3
# 初始化參數,考慮偏置項
theta = np.random.randn(3, 1)
iterations = 1000
alpha = 0.01
# 損失函數
def compute_cost(X, y, theta):
m = len(y)
predictions = X.dot(theta)
cost = (1 / 2 * m) * np.sum(np.square(predictions - y))
return cost
# 梯度下降
def gradient_descent(X, y, theta, alpha, iterations):
m = len(y)
cost_history = np.zeros(iterations)
for i in range(iterations):
gradients = X.T.dot(X.dot(theta) - y) / m
theta = theta - alpha * gradients
cost_history[i] = compute_cost(X, y, theta)
return theta, cost_history
# 添加偏置項
X_b = np.c_[np.ones((len(X), 1)), X]
# 運行梯度下降
theta, cost_history = gradient_descent(X_b, y, theta, alpha, iterations)
# 結果可視化
plt.plot(range(1, iterations + 1), cost_history, 'b-')
plt.xlabel('迭代次數')
plt.ylabel('損失值')
plt.title('梯度下降優化損失值')
plt.show()
print(f"優化后的參數: {theta.ravel()}")背景:
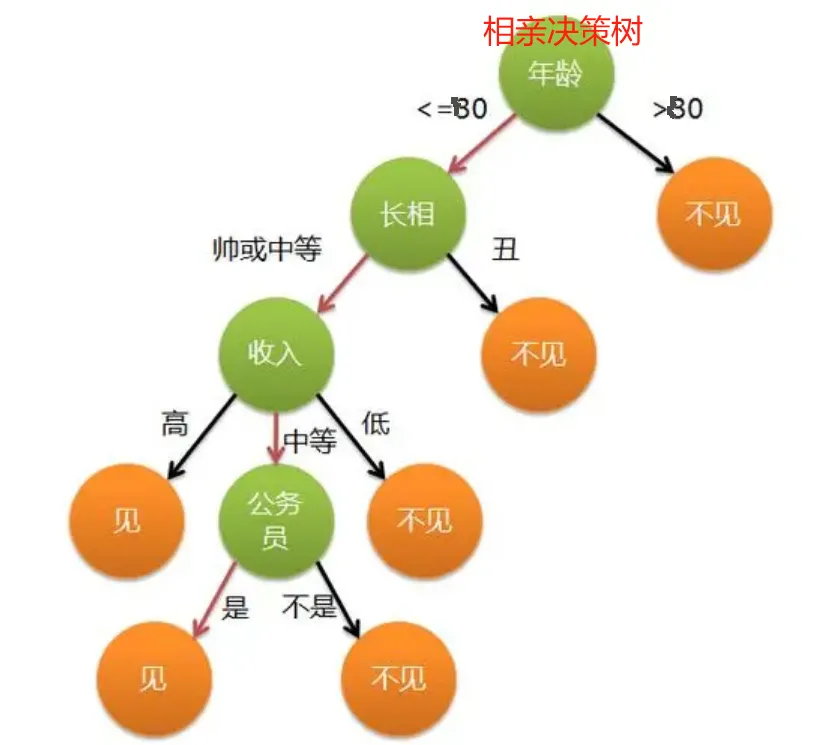
決策樹(Decision Tree)是一種基于樹形結構的監督學習算法,用于分類和回歸任務。決策樹算法最早由 Ross Quinlan 在 20 世紀 80 年代提出,包括經典的 ID3、C4.5 和 CART 算法。決策樹的直觀和易于解釋的特點,使其在金融、醫療和市場營銷等領域得到了廣泛應用。
原理:
決策樹通過遞歸地將數據集分割成更小的子集來構建樹狀模型。每個內部節點代表一個特征,每個分支代表該特征的一個取值,每個葉節點代表一個類別或預測值。決策樹的構建過程包括以下步驟:
信息增益:信息增益用于衡量某一特征對數據集進行分割時所帶來的信息熵的減少。信息熵(Entropy)表示數據集的純度,計算公式為:

基尼系數:基尼系數(Gini Index)用于衡量數據集的不純度,計算公式為:
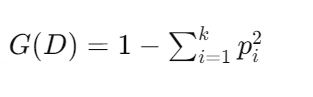
優缺點:
優點:
缺點:
應用場景:
決策樹在金融、醫療、市場營銷等領域有廣泛應用。以下是一些具體的應用場景:
案例分析:
讓我們來看一個具體的案例:使用決策樹進行客戶分類。假設我們有一個數據集,其中包含客戶的年齡、收入和購買情況(0 表示未購買,1 表示購買)。我們可以使用決策樹來建立客戶特征與購買情況之間的關系模型。
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
import matplotlib.pyplot as plt
import numpy as np
# 生成武俠風格的數據,確保所有特征值為正數
X, y = make_classification(n_samples=200, n_features=2, n_redundant=0, n_informative=2,
n_clusters_per_class=1, random_state=42)
X += np.abs(X.min()) # 平移數據確保為正
# 將數據集分為訓練集和測試集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
# 創建決策樹模型,并設置最大深度為3
dt = DecisionTreeClassifier(max_depth=3)
# 訓練模型
dt.fit(X_train, y_train)
# 繪制數據點和決策邊界
def plot_decision_boundary(model, X, y):
# 設置最小和最大值,以及增量
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.01),
np.arange(y_min, y_max, 0.01))
# 預測整個網格的值
Z = model.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
# 繪制決策邊界
plt.contourf(xx, yy, Z, alpha=0.4)
# 繪制不同類別的樣本點
plt.scatter(X[y == 0][:, 0], X[y == 0][:, 1], c='red', marker='x', label='普通武者')
plt.scatter(X[y == 1][:, 0], X[y == 1][:, 1], c='blue', marker='o', label='武林高手')
plt.xlabel('功力值')
plt.ylabel('內功心法')
plt.title('武俠世界中的武者分類圖')
plt.legend()
# 繪制決策邊界和數據點
plot_decision_boundary(dt, X, y)
plt.show()這段代碼首先生成了一組包含200個樣本的武俠風格數據,每個樣本有兩個特征:功力值和內功心法,目標是分類武者是否為武林高手。
然后,我們使用DecisionTreeClassifier創建了一個決策樹模型并對其進行訓練。
通過定義plot_decision_boundary函數,我們繪制了模型的決策邊界,并使用不同顏色和形狀標記來區分普通武者和武林高手,直觀地展示了決策樹在二分類任務中的分類效果。
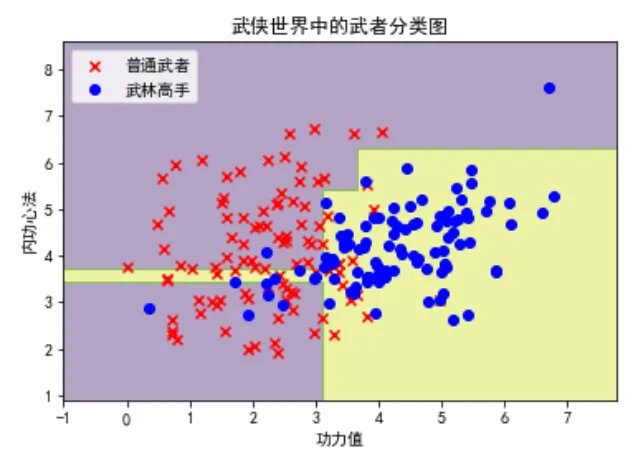
(你可以修改 max_depth 看看有什么變化)
背景:
神經網絡(Neural Networks)起源于 20 世紀 40 年代,由 Warren McCulloch 和 Walter Pitts 提出。他們的工作靈感來源于人腦的結構和功能,希望通過數學模型模擬生物神經元的工作方式。神經網絡的發展經歷了多次起伏,直到 2006 年 Geoffrey Hinton 等人提出深度學習(Deep Learning)的概念,神經網絡才重新獲得關注,并迅速成為人工智能領域的熱點。
原理:
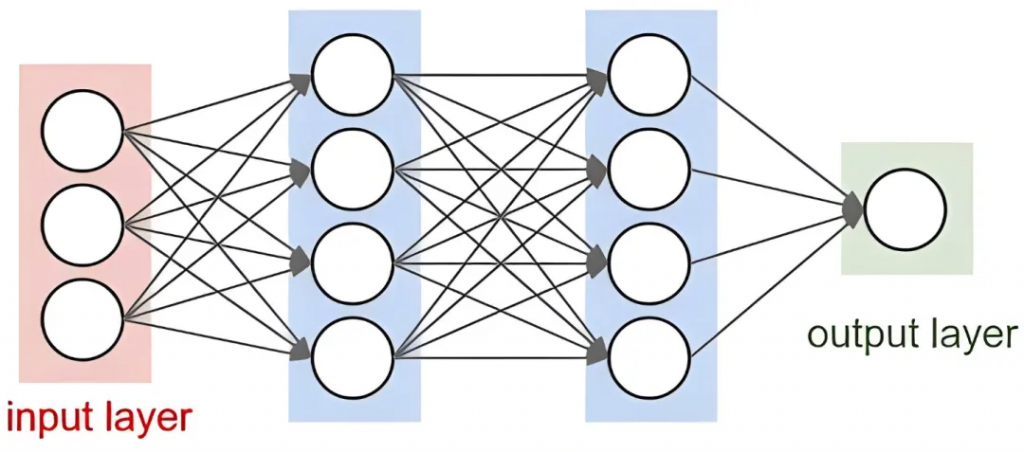
神經網絡由多個層級的節點(神經元)組成,每個節點通過加權連接傳遞信號。一個典型的神經網絡結構包括輸入層、隱藏層和輸出層。輸入層接收原始數據,隱藏層通過加權求和和激活函數處理數據,輸出層生成最終的預測結果。每層節點的輸出由前一層節點的加權和通過激活函數計算得到:
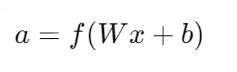
其中,( a ) 是輸出,( W ) 是權重矩陣,( x ) 是輸入向量,( b ) 是偏置向量,( f ) 是激活函數。
激活函數:
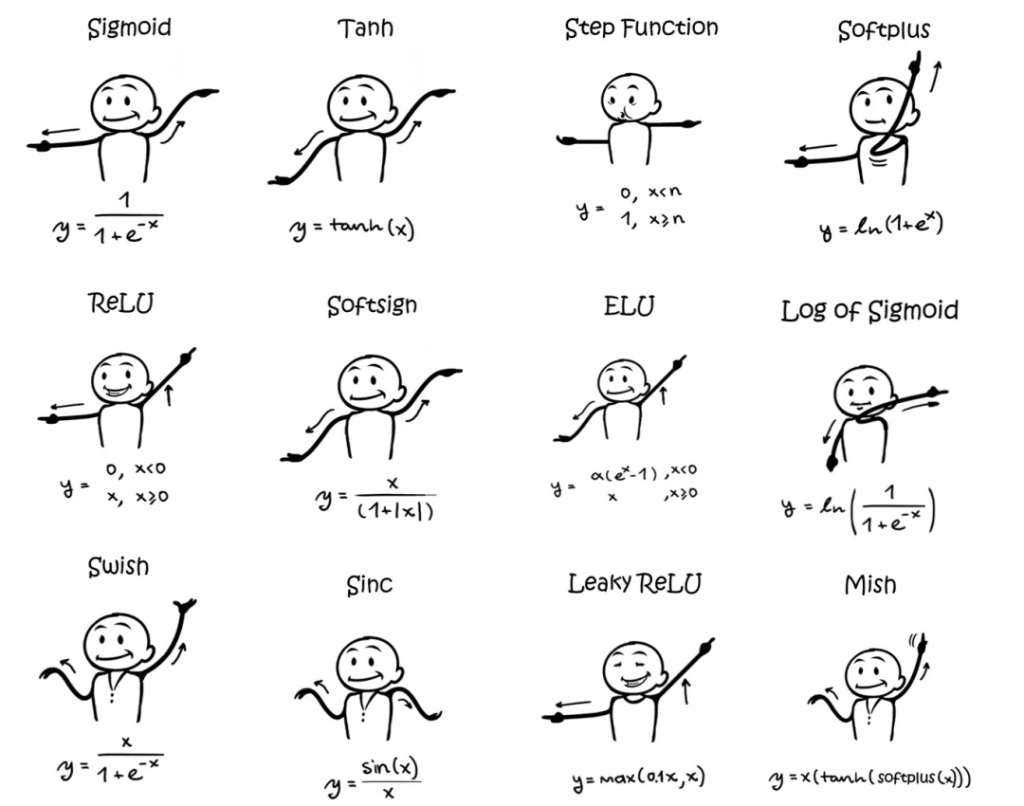
訓練: 神經網絡通過反向傳播算法(Backpropagation)進行訓練。反向傳播通過計算損失函數的梯度,調整網絡中的權重和偏置,以最小化預測誤差。訓練過程包括以下步驟:
優缺點:
優點:
缺點:
應用場景:
神經網絡在圖像識別、語音識別、自然語言處理等領域有廣泛應用。以下是一些具體的應用場景:
案例分析:
讓我們來看一個具體的案例:使用神經網絡進行手寫數字識別。假設我們使用經典的 MNIST 數據集,其中包含 28×28 像素的手寫數字圖片,每張圖片對應一個數字標簽(0-9)。
import tensorflow as tf
from tensorflow.keras.datasets import mnist
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Flatten
from tensorflow.keras.utils import to_categorical
# 加載數據
(X_train, y_train), (X_test, y_test) = mnist.load_data()
# 預處理數據
X_train = X_train.reshape(-1, 28 * 28) / 255.0
X_test = X_test.reshape(-1, 28 * 28) / 255.0
y_train = to_categorical(y_train, 10)
y_test = to_categorical(y_test, 10)
# 創建模型
model = Sequential([
Flatten(input_shape=(28 * 28,)),
Dense(128, activation='relu'),
Dense(64, activation='relu'),
Dense(10, activation='softmax')
])
# 編譯模型
model.compile(optimizer='adam', loss='categorical_crossentropy', metrics=['accuracy'])
# 訓練模型
model.fit(X_train, y_train, epochs=10, batch_size=32, validation_split=0.2)
# 評估模型
loss, accuracy = model.evaluate(X_test, y_test)
print(f"Test Accuracy: {accuracy:.4f}")在這個例子中,我們使用 TensorFlow 和 Keras 庫創建了一個簡單的全連接神經網絡,用于識別手寫數字。通過訓練模型,我們可以在測試數據上評估其準確性,并可視化模型的性能。
背景:
K均值聚類(K-means Clustering)是一種常用的無監督學習算法,用于將數據集劃分為 K 個互斥的簇。該算法由 Stuart Lloyd 于 1957 年在電話信號處理研究中首次提出,1967 年由 James MacQueen 正式命名并推廣應用。K均值聚類在許多領域得到廣泛應用,如圖像處理、市場營銷、模式識別等。

原理:
K均值聚類通過迭代優化的方法,將數據點分配到 K 個簇中,使得每個簇內的數據點與簇中心(質心)之間的距離平方和最小化。具體步驟包括:
算法的目標是最小化以下目標函數:

優缺點:
優點:
缺點:
比如下圖數據分布,使用 K-means 的效果就很憂傷了
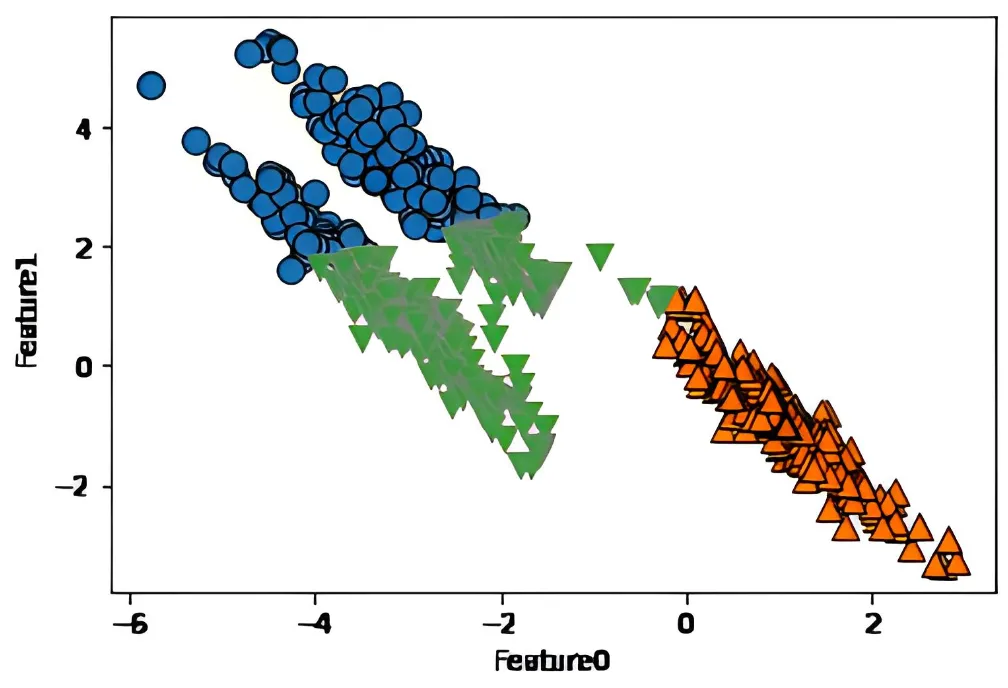
應用場景:
K均值聚類在市場營銷、圖像處理、模式識別等領域有廣泛應用。以下是一些具體的應用場景:
案例分析:
讓我們來看一個具體的案例:使用K均值聚類進行客戶分類。假設我們有一個數據集,其中包含客戶的年齡和收入。我們可以使用K均值聚類將客戶分為三個群體。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
# 示例數據
data = {
'age': [25, 45, 35, 50, 23, 31, 22, 35, 42, 51],
'income': [50000, 100000, 75000, 120000, 40000, 60000, 45000, 80000, 110000, 130000]
}
df = pd.DataFrame(data)
# 創建K均值模型
kmeans = KMeans(n_clusters=3)
kmeans.fit(df)
# 預測聚類結果
df['cluster'] = kmeans.labels_
# 可視化聚類結果
plt.scatter(df['age'], df['income'], c=df['cluster'], cmap='viridis')
plt.xlabel('Age')
plt.ylabel('Income')
plt.title('Customer Segments')
plt.show()
print(df)在這個例子中,我們使用 sklearn 庫中的 KMeans 模型來對客戶的年齡和收入進行聚類。通過訓練模型,我們可以將客戶分為三個群體,并可視化聚類結果。同時,可以輸出每個客戶的聚類標簽。
[ 抱個拳,總個結 ]
線性回歸,一種簡單而有效的回歸算法,
邏輯回歸,一種簡單而有效的分類算法,
梯度下降,一種基本且重要的優化算法,
決策樹,一種直觀且易于解釋的機器學習模型,
神經網絡,一種強大的深度學習模型,
K均值聚類,一種簡單高效的無監督學習算法,
這些基礎算法構成了機器學習的核心,無論是線性回歸的簡潔性,還是神經網絡的復雜性,都展示了它們在不同應用場景中的價值。同時,這些算法正被不斷改進和創新,Enjoy
原文轉自 微信公眾號@算法金